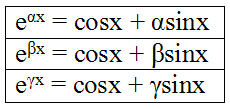Многополярная волновая функция
Функциональный анализ
Необходимость рассмотреть математический аппарат волновой функции Шрёдингера появляется в связи с её частным случаем и не носит особый характер угождения современным теориям. Тем не менее, здесь будет показано, что волновая функция в уравнении Шрёдингера всего лишь частный (и достаточно скудный) случай.
Волновая функция в уравнении Шрёдингера
Волновая функция это функция состояния, пси-функция, или амплитуда вероятности представлена как комплексная функция, используемая в квантовой механике для вероятностного описания состояния квантовомеханической системы. В широком смысле — то же самое, что и вектор состояния.
Вариант названия «амплитуда вероятности» связан со статистической интерпретацией волновой функции: вероятность нахождения частицы или физической системы в данном состоянии равна квадрату абсолютного значения амплитуды вероятности этого состояния. Что это означает?
В качестве функции ψ берётся квадрат модуля сопряженного комплексной функции.
Напомню.
Комплексная функция — функция, которую можно представить в виде f(x) = u(x) + iv(x), где i — это «мнимая» единица, а u и v — действительные функции. Функция u(x) называется действительной частью функции f(x), а iv(x) — её мнимой частью.
Функция f*(x) = u(x) – iv(x) называется комплексно сопряжённой функции f(x) = u(x) + iv(x)
Произведение функции на её комплексно сопряжённую называется квадратом модуля функции. Квадрат модуля функции всегда положителен и обозначается как Ψ. |f(x)|2 = f(x) f*(x) = u(x)2 + v(x)2
Вот это и есть база функции Шрёдингера. Дальше пойдут решения и вариации.
Волновая функция Ψ(х1,х2, …хn) зависит от координат (или обобщённых координат) системы и формируется таким образом, чтобы квадрат её модуля Ψ(х1,х2, …хn)2 представлял собой плотность вероятности обнаружить систему в положении, описываемом координатами х1 = x01, x2 = x02, …, xn = xon
Набор координат, которые выступают в роли аргументов функции, представляет собой полный набор физических величин, которые можно измерить в системе. В квантовой механике возможно выбрать несколько полных наборов величин, поэтому волновая функция одного и того же состояния может быть записана от разных аргументов. Выбранный для записи волновой функции полный набор определяет представление волновой функции. Так, возможны координатное представление, импульсное представление, в квантовой теории поля используется вторичное квантование и представление чисел заполнения или представление Фока и другие.
Если волновая функция, например, электрона в атоме, задана в координатном представлении, то квадрат модуля волновой функции представляет собой плотность вероятности обнаружить электрон в той или иной точке пространства. Если эта же волновая функция задана в импульсном представлении, то квадрат её модуля представляет собой плотность вероятности обнаружить тот или иной импульс.
Для волновых функций справедлив принцип суперпозиции, заключающийся в том, что если система может пребывать в состояниях, описываемых волновыми функциями Ψ1 и Ψ2 , то она может пребывать и в состоянии, описываемом волновой функцией ΨΣ = c1 Ψ1 + c2 Ψ2 при любых комплексных c1 и c2.
Что если заменить базу?
Варианты сопряжений
В книге «Зарождение Новых Миров» В.Ленский предлагает многополярные алгебры (см. также Многополярные алгебры) , в которых алгебра «комплексных переменных» - всего лишь частный примитивный случай.
Могут ли быть не поляризованные состояния, которые здесь называют «действительными числами» в случаях, когда сопряженных состояний окажется не два, а, например, три?
В пример можно привести взаимодействие трёх полярностей, в которых «сопряженное число» и есть исходное число:
(ι + j + k)*(ι +j + k) = ι2 +j2 + k2 + 2(ι j + ι k + j k).
Если найдём пространство, в котором ι j + ι k + j k = 0, то (ι +j + k)2 = ι2 +j2 + k2.
Дальше зависит от пространства.
Если в алгебре участвовало три изоморфных двухполярных пространства, то ι2 = j2 = k2 = 1. Откуда (ι +j + k)2 = 3.
Если в алгебре участвовало три изоморфных трёхполярных пространства, то (ι +j + k)2 = α + β + γ, где α2 = ι, β2 = j, γ2 = k, ιjk = 1. αβγ = 1.
Записано для наглядного сравнения с «кватернионами» (хотя «кватернионы» – система противоречивая).
Такое возможно, так как в таком пространстве ιj = k2, ιk = j2, jk = ι2. ι j + ι k + j k = k2 + j2 + ι2 . Отсюда для (ι +j + k)2 = ι2 +j2 + k2 + 2(ι j + ι k + j k) будет (ι +j + k)2 = 3(α + β + γ).
Умножаем (α + β + γ) (ι +j + k) = 3.
Здесь (ι +j + k)3 = 3, то есть «абсолютное» число 3 образовалось при взаимодействии шести полярностей.
Итак,
1. неполяризованные числа («абсолютные числа») есть результат взаимодействия полярностей, но не самих чисел;
2. сопряженными могут быть не только две функции «комплексных переменных», как в базе уравнения Шрёдингера. Их может быть три, пять, шесть и вообще любое число;
3. уравнение Шрёдингера становится частным случаем для двух сопряженных функций.
Сопряжение экспонент
Возьмём другой бытующий сегодня вариант, когда сопряжение и комплексные переменные выражены экспонентами. Например, решение волнового уравнения представлено в виде суммы падающей и отражённой волны ψ = ℮(ikz) + a℮(- ikz) где i и –i суть сопряженные «мнимые» числа.
В «Зарождении Новых Миров» (см. также Многополярные алгебры) приведены множество сопряженных переменных на базе экспоненты. Например, в приложении предыдущему примеру, где (ι +j + k)2 = 3(α + β + γ).
Можно найти пространство трёх изоморфных двухполярных алгебр, где (еαх)(еβх (еγх) = е (α + β + γ)x.
С другой стороны, еαх еβх еγх = cos3x + sin3x .
С учётом предыдущего е (α + β + γ)x = cos3x + sin3x.
Из этой же алгебры следует, что ψ = еαх + aеβх +bеγх, где α, β, γ – сопряженные.
В итоге получили действительные числа не только от трёх полярностей, но и их кубы «абсолютных» чисел.
Этих примеров достаточно, чтобы показать, что двухполярных «кошка жива» и «кошка мертва» не достаточно для описания квантовомеханических процессов. Вероятностных состояний будет столько, в каком пространстве происходит процесс.
Многополярная волновая функция
Итак, в выбранном пространстве для функции f(x) = u(x) + iv(x) + …+kw(x) найдётся сопряженная функция f*(x) = u(x) + αv(x) + …+δw(x) такая, что |f(x)|2 = f(x) f*(x) = u(x)2 + v(x)2 + …+ w(x)2
Более того, могут оказаться три и более «сопряженных» функций. Тогда, для сопряженных
f(x) = u(x) + iv(x) + …+kw(x)
f*(x) = u(x) + αv(x) + …+δw(x)
…………………………………….
fn*(x) = u(x) + φv(x) + …+λw(x)
будет справедливо выражение
|f(x)|n = f(x) f*(x)… fn*(x) = u(x)n + v(x)n +… λw(x)n
В результате, для волновой функции в многополярном пространстве (а не только в «комплексном», как сейчас) будет иметь вид:
|f(x)|n = f(x) f*(x)… fn*(x) = u(x)n + v(x)n +… λw(x)n
Кстати, рекомендую посмотреть опровержение Великой Теоремы Ферма в книге «Зарождение Новых Миров» а также Многополярные алгебры. Там разбираются случаи, например, для многополярного «нормирования», когда три и более сопряженных функции выраженные как:
f(x) = u(x) + iv(x)
f*(x) = u(x) + αv(x)
………………………
fn*(x) = u(x) + φv(x)
В результате дают:
|f(x)|n = f(x) f*(x)… fn*(x) = u(x)n + v(x)n