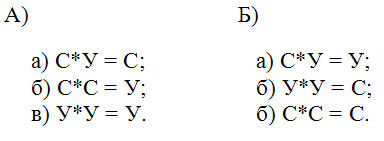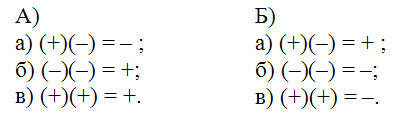Алгебры двyх пространств
1. Класс с единицей 0 может иметь собственные полярности.
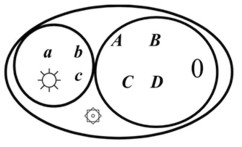
Запишем для класса с единицей ☼ и полярностями а, b, с закон а* b* с = ☼. Точно так же для класса с единицей 0 и полярностями A, B, C, D будет A + B + C + D = 0. Одновременно, как раньше было показано, а + b + с + ☼ = 0.
2. Это две изоморфные системы полярных отношений. Теперь они при введении в единый класс теряют свойство изоморфизма и становятся тождественными в различии.
3. Из предыдущего ясно, что класс с единицей ☼ выполняет законы отношений в этом классе. Например, а* b* с = ☼. Класс с единицей 0, тоже выполняет отношения этого класса. Например, A*B*C*D = 0.
Как соотносятся полярности разных классов?
Если между классами устанавливается отношение двух интенсивностей связей, то возможны варианты:
а) асимметричная алгебра, где в одном из пространств выполняется «умножение», а в другом – «сложение»;
б) алгебры, где симметрично происходят взаимодействия так, что, если в одном из них совершается «умножение», то эти полярности в другом пространстве совершают «сложение»;
в) пространства приобретают новый класс с охватывающей единицей ۞.
г) единицей может быть группа полярностей, или поляризованных объектов.
В современной арифметике и алгебре известен закон дистрибутивности, в котором для элементов а, в, с можно записать (а + в)с = ас + вс.
Если а* b* с = ☼ и A + B + C + D = 0, то интерес представляет отношение между полярностями разных пространств.
Что будет, например, в результате взаимоотношения а*А? Во-первых, это не может быть полярность из пространства «умножение». Однако возможно а*А = В. Тогда возьмём а*В = А, а*С = В, а*D =
Преимуществ у тех или иных полярностей нет, а общность классов полагает наличие охватывающего класса с единицей ۞. Поэтому в записи, например, (А + В)*а будет Аа + Ва. Если по привычке не смотреть на знак + как на «сумму», то эта запись очевидна и без доказательств, так как три объекта взаимодействуют друг с другом. Чтобы снять негативную привычку запишем отношение в классе с единицей 0 как (А)(В) и теперь (А) (В)*а. Естественно, что эти полярности должны «прореагировать» друг с другом. Поэтому (А)(В)*а = (Аа)(Ва).
4. Другое дело, если (А)(В)*(a)(b) = (Aa)(Ab)*(Ba)(Bb).
Теперь в привычной записи (А + В)*(a + b) = (Aa + Ab + Ba + Bb).
Записан известный закон дистрибутивности. Кстати, его можно логически доказать (кстати, его можно доказать, а не постулировать, как это сделано в современной математике), если исходить из свойств двух различающихся классов, охваченных в единый класс.
5. Тема двух различающихся классов озвучивается не случайно. Ещё раньше математики должны были догадаться, что, вводя во взаимоотношения «умножение» и «сложение», фактически получают кроме алгебры, новый класс, с новой единицей. Либо один из классов становится полностью «полярным» объектом, а другой – единицей.
6. Если до этого мы имели дело с «расширением» существующих алгебр с операциями «сложение» и «умножение» и вместо двухполярности получили разнообразие поляризованных пространств и алгебр в них, то теперь образуется некоторое «растекание».
7. Чем отличается такое «растекание»? В конкретном пространстве каждый объект взаимодействует не с одним, а единовременно с двумя объектами.
8. Выразим теперь весь класс как некоторый объект. В современных алгебрах имеется два таких объекта «сложение» (С) и «умножение» (У). Следовательно, они представятся как двухполярная лока операций. По законам локи 2 отношения между полярными объектами («сложением» и «умножением») будут: А) в первом случае, когда умножение (У) примет роль единицы; Б) во втором случае, когда сложение (С) станет единицей.
9. Из двух альтернативных вариантов в арифметике, а затем, алгебрах выбрали случай А). Если вспомнить, то из двух альтернативных правил умножения А) и Б)
была выбрана система отношений А). Система Б) умом всё же используется, но в альтруистических и религиозных концепциях. Например, для (–)(–) = –, считая «минус» отрицательным, можно сказать «уничтожение зла это всё же зло». Специально это рассмотрено в разделе «Виды ума».
10. Как понимать системы операций А) и Б)? С*У = С мы встречаем в законе дистрибутивности так, что в ходе взаимодействий полярностей «умножения» и «сложения» итоговые полярности остаются в «сложении».
Например, (а + b)(c + d) = ac + bc + ad + bd. Если каждому произведению поставить в соответствие элемент, то есть, ac = e; bc = f; ad = g; bd = h, то получим e + f + g + h.
11. Операция С*С = У будет понятна из примера: 4 + 4 + 4 + 4 = 4 х 4 = 42.
12. Операция У*У = У понятна из того, что (а)(в)с = авс.
13. Для контраста рассмотрим альтернативную систему операций Б). Выражение У*У = С можно выразить примером 4 х 4 х 4 х 4 = 4 + 4. Необычно? Нет, не привычно.
14. Правомочность альтернативных, но не совместимых, систем отношений занимает своё место тогда, когда их «равноправие» вынуждает искать такой компромисс, когда противоречия не будет. Этот компромисс найден в диалектике и в трёхполярном виде ума. В диалектике «добро» и «зло» приводятся к единству, а в трёхполярном уме две несовместимые двухполярные системы А) и Б) переходят в трёхполярную.
15. Изоморфных лок поставленных в отношении друг к другу могло бы быть три. Например, если бы современная алгебра была представлена двумя различающимися классами, включёнными в один класс, то появилась бы ещё одна единица. Преимуществ у тех или иных полярностей нет, а общность классов полагает наличие охватывающего класса с единицей ۞.
16. Если в новом классе законы определены то, какие будут отношения с новой единицей? Более того, если в новом классе тоже есть полярные элементы, то какие взаимоотношения установятся с ними? Впрочем, сначала закономерно выйдем из ограничения Законом Сброса.