Алгебра

Ревизия

История

Развитие научной мысли двигалось так, что постепенно поляризация объектов мышления в математике увеличивалась. Сначала ввели «отрицательные» числа. Это тут же чётко выделило «абсолютные» числа как не поляризованное. Фактически абсолютные и натуральные числа это одно и то же, то есть не поляризованные числа. К сожалению, «абсолютные» числа склеили с «положительными». Это стало тормозить развитие полярных отношений.

В арифметике появляется три полярности +, -, 0, но в «умножении» ещё две: +, –, так, что а) (+)*(+) = +, б) (+)*(–) = –, в) (–)*(+) = –, г) (–)*(–) = +.

Алгебра добавляет деление и тем самым, третью полярность в «умножении». Из а/а = 1 ещё не следует поляризации, но а/-а = -1, уже появляется +, –, е, Здесь элемент е вытесняет предыдущий +. Если в алгебре «действительных чисел» (+)*(+) = +, то теперь в теории групп (е)*(е) = е. Дали название е как «единица».

Появилась необходимость ввести термин «идемпотентный элемент». Вместе с арифметикой будет: 0 + 0 = 0, (+)*(+) = +, (е)*(е) = е. Заметили ли математики, что деление и появление «единицы» увеличило число полярностей с двух до трёх? Нет.

Следующим ходом к арифметическим трём полярностям +, –, 0 добавляются «мнимые» числа, как следствие необходимости извлекать «корень квадратный» из отрицательно поляризованных чисел. От неожиданности новые числа назвали «мнимыми». Как и деление, извлечение корня «растягивает» область полярных чисел. Теперь появляются «кватернионы». Четыре полярности ί, j, k, + составляют четырёхполярное пространство.

У.Гамильтон изобретает «кватернионы» путем введения в суперпозицию трёх изоморфных систем «комплексных» чисел, но с огромным противоречием в самой системе отношений. Напрасно математики спасали эту систему, так как в ней доказвается, что + = – , ί = –ί, j = –j, k = – k . Никакая альтернативность умножения эту систему не спасёт. Иначе, можно изобретать всё, что хочешь, нарушая принцип математики – аксиоматичность и чёткость доказательств.

Три фактора сковали творческую мысль математиков: а) арифметика, которая напрямую связана с действительностью (поэтому числа четырёхполярности назвали «мнимыми»); б) невнимательность, поэтому не заметили даже то, что деление и извлечение корня увеличивает число полярностей; в) неаккуратность, по причине которой, законы, полученные в найденном варианте отношений, тут же подражанием распространялись во все области математики.

Натуральные числа это не «положительные» числа. «Положительное» число поляризовано в совокупности с «отрицательным». Поэтому, безотносительные 15 лошадей могут поляризоваться так, что 10 лошадей «моих», а 5 лошадей «чужие». Если мы производим операцию 15 – 5 = + 10, так как +10 и – 5 уже поляризованные числа. Безотносительные числа лучше называть «натуральными».

Пока в арифметике безотносительное констатирование факта наблюдений (15 лошадей, три озера, двадцать журавлей), то там нет алгебры. Но уже в арифметике начинается вычитание, то есть тут же числа поляризуются. Алгебра имеет дело не с натуральными, а с поляризованными объектами и числами. Натуральные числа тут безынтересные.

Великая ли Великая теорема Ферма?

Великая теорема Ферма (также Последняя Теорема Ферма) утверждает что «для любого целого числа n > 2 уравнение не имеет положительных целых решений a, b, c. »

Это, наверное, самая знаменитая теорема во всей математике. Теорема была сформулирована Пьером Ферма в 1637 на полях книги «Арифметика» Диофанта с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было здесь поместить. История Великой теоремы Ферма неразрывно связана с историей математики, так как затрагивает все основные темы теории чисел.

И всё же, великая ли Великая теорема?

Когда Пифагор доказывал свою теорему о прямоугольном треугольнике в котором где a, b – катеты, c – гипотенуза, то он брал натуральные числа площади. Другое дело – алгебра. Например, для нахождения катета придётся применить отрицательные числа. Извлечение корня квадратного даст нам два катета «положительный» и «отрицательный». Гипотенуза тоже может быть «положительной» и «отрицательной». Это означает, что в пространстве находятся не один, а два треугольника, то есть треугольник «расщепился». При доказательствах теоремы Ферма каждый математик использовал алгебру поляризованных чисел, а не натуральные числа. Подгонка? Не исключено. Скорее, неосмысленное оперирование. В итоге теорема Пифагора к алгебрам не имеет отношения, так как математики упражнялись не с натуральными величинами площадей, а с поляризованными числами.

Ну, а, если алгебра будет не двухполярной? Тогда мы получим не два треугольника со сторонами + и – , как в двухполярных преобразованиях имели математики 369 лет, а три треугольника.

• 1. Возьмём трёхполярное пространство, то есть «расщепим» треугольник не на два, как это делают математики, а на три. Тогда, вместо полярностей +, – обозначим три полярности: + ,ί, j. В такой алгебре 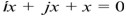, а так же (ί)*(j) = +.

• 2. Проведём такие математические преобразования, чтобы охватить несколько разделов математики (дабы не тратить впустую время на каждый раздел).

а) К тригонометрическим функциям: (cos x +sin x)*(cos x +ί sin x)*(cos x +j sin x) ,

b) К показательной функции: .

с) В связи этих функций :

,

,

,

d) Окончательно из a), b), c) получим .

е) Поскольку cos x = b/c, sin x = а/c , где a, b – катеты, с – гипотенуза, то заменим формулу d).

f) В итоге получим: .

• 3. Аналогично легко доказать для алгебр с нечётным числом полярностей.

.

Это опровергает «Великую» теорему Ферма.

Иными словами, теорема Ферма остаётся Великой лишь в частном случае алгебры двухполярных отношений. А, так как, полярных пространств очень много, то Великое превращается в малое и частный случай.

• Примечание.

Поступило возражение, что экспонента в степенн х не есть cosx + sinx. Замечание можно принять только щадя привычки тех, кто прикрепил себя к законам двухполярной математики. Можете взять i, j, k так, что i + j + k = 0 . Затем написать соответственно экспоненты в степенях iх, jх, kх. Теперь получите опровержение "Великой" Теоремы Ферма.

Кстати, это возражение заслуживает внимание в том, что отныне обязательно найдётся лока, в которой выполнятся "невыполнимые" преобразования. Например, можно доказать, что четвёртые степени а и b в сумме дают с в четвёртой степени: . Этим будет показано, что Великая Теорема Ферма не состоятельна и для чётных степеней чисел.

Особо подчеркну, что речь не идёт о мнимых числах или специальных cosx и sinx . Речь идёт о пространствах, отличающихся от двухполярного. Там всё такое же действительное. О таких пространствах см. раздел Геометрия.

Анализ

По сути, алгебра это взаимодействие лок с разными видами связей. Например, +7 - 7 = 0 это фрагмент плоскостной локи 3. Трёхполярное пространство вошло в алгебру "действительных чисел" как составная часть. В то же время при делении +7 : -7 = -1 это фрагмент локи 3 объёмной поляризации.

Однако в алгебре "действительных чисел" используется сочетание: трёхполярное пространство в "сложении" такое, что +а - а = 0, и двухполярное - в "умножении" такое, что а) (+)*(+) = +, б) (+)*(-) = -, в) (-)*(+) = -, г) (-)*(-) = +

Отсюда алгебра таких лок будет, например, (а - в)*(-с) = - аc + вс . Конечно, закон дистрибутивности выведен на базе арифметического опыта и обобщен в алгебре.

Имея не внимательный опыт предшественников, к видам взаимодействия подойдём аккуратно. Например, из а + в = с, совершая перенос через знак равенства, знак числа меняют на обратный, то есть а = в - с. Это правило не правомерно в иных локах.

Внимание! Особо напомню, что всякий раз мы имеем дело с натуральными числами и объектами. Поэтому названия "действительные числа", "комплексные числа" пусть вас не смущают. Так математики назвали двухполярные и четырёхполярные натуральные числа. Никакой "мнимости" в таких числах нет. Есть поляризованность чисел и объектов, относящая к тому или иному пространству, с тем или иным числом полярностей.

Алгебра полярностей

1. Возьмём в пример некоторые полярности ί, j, k, 0 в плоскостной поляризации и ί, j, k, ☼ в объёмной поляризации. В этих локах, так же как и в трёхполярных, где +1 - 1 = 0 (здесь полярности +, -, 0)будет 1ί + 1j + 1k = 0 . Произвольно выберем суперпозиционную локу 4. Здесь (ί)*(ί) = +, (j)*(j) = +, (k)*(k) = + , (ί)*(j)*(k) = +.

2 Проведём алгебраическое преобразование, например (1ί + 1j + 1k)*(1ί + 1j + 1k) = +3. Иными словами, возведение в степень и проведение алгебраических преобразований привело нас к числу 3. Если по условию 1ί + 1j + 1k = 0, то фактически мы провели операцию (0)*(0) = +3 , где + - единица в суперпозиционной локе 4.

3. Итак, слепо следовать правилу в умножении 0х0 = 0 тоже не следует.

Прикладные алгебры

Так уж повелось, что не разобравшись с тем, что математика имеет в алгебре "действительных чисел" дело с поляризованным пространством, стали применять двухполярную алгебру и в естественных науках.

Откликнется ли физика, или, например, релятивистская механика, на двухполярность? Сомнительно, что вся Вселенная поляризована только на два вида полярностей.

Взять, к примеру, Теорию Относительности А.Эйнштейна. Там сразу же постулируется с + с = С. Иными словами, скорость света приобретает роль единицы. Но увы, применяются в преобразованиях Лоренца операции алгебры "действительных чисел", то есть алгебры двухполярных отношений. Более того, в преобразованиях извлекается квадратный корень, а это "расщепляет" пространство до четырёх полярностей. Получается по преобразованиям Лоренца, что свет "перетекает" из двухполярное пространство в четырёхполярное.

Единицаимеет место в каждом пространстве с любым числом полярностей. Эйнштейн не определил само пространство. В качестве оговорки замечу, что область света принадлежит анализатору зрения, где выполняются не двухполярные, а, как минимум, трёхполярные законы.

Проведём преобразование "перетекания" из трёхполярного в шестиполярное пространство.

Соответственно, преобразования Лоренца запишем так, что х = γ(х + vt),будет поляризоваться не на + и -, а на +, ί, j, то есть, например, Х = (х + ίvt). Так как х = ct, то для полярности, например ί будет ct = (ct + ίvt). Как и в примере с теоремой Ферма, решая систему уравнений, получим .

После несложных преобразований (см. Основы многополярности), получим коэффициент преобразования пространства и времени. .

Окончательно при v = c, то есть при достижении объектом скорости света будет: .

Вновь мы встречаемся с неожиданным результатом. Оказывается, что при приближении скорости движущегося тела к скорости света нет никакого парадокса близнецов . Нет и стремления времени к нулю . Нет бесконечной массы. Так что фантазёры поторопились. Почему? Область существования света -вовсе не двухполярное пространство.

Многоликость света (семиполярного пространства) такова, что он некоторым образом и весьма частично содержит двойственные отношения, но в иной форме, чем предлагает алгебра "действительных чисел" и преобразования Лоренца и Минковского (четырёхмерный континиум). Поэтому некоторым образом свет может "искривляться" в магнитном поле земли.

Конечно, искажения, как и должно быть при переходах из пространство в пространство, есть. Но оно чётко соизмеримое.

---