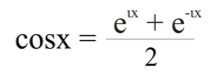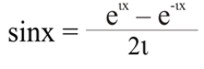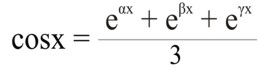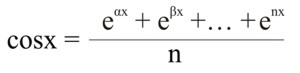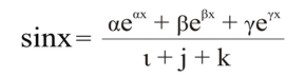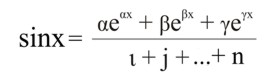Тригонометрические формулы Эйлера и Ленского
Формулы Эйлера
Для функций комплексной переменной известна формула Эйлера, где из еιх = cosx + ιsinx, а так же е-ιх = cosx – ιsinx получают еιх + е-ιх = 2cosx.
Откуда
Точно так же получим для sinx.
еιх – е-ιх = 2ιsinx.
Так как математики не заметили факт расщепления двухполярности до четырёхполярности, то, естественно, пропустили многообразие алгебр, где формула Эйлера есть частный случай, относящийся только к четырёхполярности.
Формулы Ленского
Если еαх = cosx + αsinx, еβх = cosx + βsinx, еγх = cosx + γsinx, то в пространстве «сложения» получим еαх + еβх + еγх = 3 cosx, так как α + β + γ = 0.
Отсюда получим выражение для cosx:
Точно так же для cosx любого числа пространств будет отношение соответствующего числа экспонент.
Если еαх = cosx + αsinx, еβх = cosx + βsinx,..., еnх = cosx + nsinx, то
еαх + еβх +...+ еnх = ncosx .
Для любого числа n изоморфных двухполярных алгебр «действительных чисел», но вошедших в непротиворечивое взаимодействие.
Если еαх = cosx + αsinx умножить на α, то получим αеαх = αcosx + α2sinx.
Аналогично βеβх = βcosx + β2sinx, γеγх = γcosx + γ2sinx.
Вводя во взаимодействие, получим αеαх + βеβх + γеγх = (α + β + γ)cosx + (α2 + β2 + γ2) sinx.
Уже рассматривались три пространства, где α + β + γ = 0. В этой же харлоке α2 = ι, β2 = j, γ2 = k.
Следовательно, αеαх + βеβх + γеγх = (ι + j + k)sinx. Окончательно
Здесь полярности α, β, γ перешли в ι, j, k по законам трёхполярного пространства.
Для любого числа n изоморфных двухполярных алгебр, вошедших в харлоку
Следует подчеркнуть, что здесь сину и косинус функции действительные.