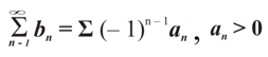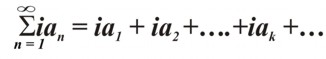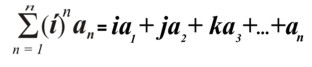Поляризованные ряды
Ряды
Всё хорошо по определению ряда как обобщение (суммирование) однополярных объектов.
Но вот появляются знакопеременные ряды. Для нас уже не секрет, что знак определяет полярность. Следовательно, появляются поляризованные числа.
В приведённом классическом случае стоит полярность (– 1).
Не склеивая полярности и вещественные объекты, получим возможность их группирования по выбранной полярности, то есть в ряде сумма будет однополярной.
Ряд может быть «знакопеременным», то есть с меняющимися полярностями. Полярности могут принадлежать только заданной локе.
Закон сброса
В таком ряде надлежит учитывать «Закон Сброса». Согласно этому закону
или то же самое
Это легко понять по аналогии с комплексными числами, где
Поэтому многополярный ряд представляет «остаток». В этом «остатке» не должно хватать одной полярности.
Итак, ряды, имеют вид:
а) группирования (суммирование) однополярных объектов;
б) группирование (суммирование) полярностей.
При группировании однополярных объектов законы отношений между объектами не меняются. Здесь могут быть «бесконечные» ряды, «сходящиеся» ряды, так как, в итоге, определится всего лишь количество данной полярности.
«Группирование» полярностей есть не что иное, как алгебра. Здесь никакой «бесконечности» и «сходимости» быть не может.