Алгебры с двумя интенсивностями связей
Сущность алгебр
В современной сатематике по причине наличия только одного двухполярного пространства простых алгебр нет. Приводятся законы отношений слитно "умножения" и "сложения".
С появрением многополярных пространств алгебры подразделяются на ПРОСТЫЕ и СЛОЖНЫЕ.
ПРОСТЫЕ алгебры описывают законы отношений в пространствах (локах). Каждому пространству соответствует своя алгебра (см. Пространства).
Примером СЛОЖНОЙ алгебры можно взять современную алгебру "действительных" или "комплексных" чисел.
В таких алгебрах проявляется разная ИНТЕНСИВНОСТЬ СВЯЗЕЙ.
Чем отличаются сложные алгебры? Введением в отношение пространств с РАЗНЫМИ и самостоятельными ЕДИНИЦАМИ. Например, в современной алгебре в "умножении" роль единицы выполняет +, а в "сложении - 0.
Характерным является то, что рождается закон дистрибутивности, когда два пространства с одинаковыми полярностями входят во взаимодействие. Это выглядит как (а + в)с + ас + вс. . Иными словами поляризованные числа одного пространства по интенсивности связи взаимодействуют с поляризованными числами другого пространства; происходит синтез пространств.
В дальнейшем будем рассматривать сложные алгебры, так как в разделе Пространства (см.Пространства) уже рассмотрены простые алгебры.
Расширение двухполярных алгебр
1. Известным случаем являются современные алгебры «действительных чисел» и «комплексных чисел». В алгебре «действительных чисел» с интенсивностью связей «умножения» два полярных состояния + и –. Одновременно с интенсивностью связи «сложение» их три: +, – , 0. Поэтому законы отношений будут именно те, которыми пользуются современные математики.
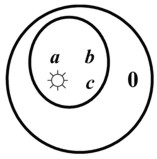
2. Рассмотрим случай, когда класс с единицей ☼ и полярностями а, b, с имеет ещё одну «охватывающую» единицу 0. Прежде всего, здесь два различающихся вида взаимодействий. Назовём их «интенсивностями связей». Поэтому можно записать а* b* с = ☼, но а + b + с + ☼ = 0.
Написанное не постулируется. Оно было доказано на понятии «класс». Действительно, с позиции нового класса, с единицей 0, все полярности и, в том числе предыдущая единица ☼, становятся полярностями этого класса.
3. Охватывающая единица 0 относится к, ставшим теперь её полярностям, а, b,…,c, ☼ так, что а + 0 = a, b + 0 = b,…,c +0 = c, ☼ + 0 = ☼. Здесь ничего нового нет. Однако как поведёт себя 0 по отношению к классу с единицей ☼?
Для класса с единицей ☼ единица 0 есть полярный элемент. Поэтому ☼*0 = 0, а* 0 = 0, b* 0 = 0,…,c*0 = 0, ☼ + 0 = ☼. Иначе не может быть по причине той, что два класса станут тождественными без различия. Иными словами, других вариантов нет. Поэтому доказывать теоремой нет смысла.
4. Подобное мы видим в современных алгебрах. Например, (+2)*0 = 0, (– b)*0 = 0, 1*0 = 0.
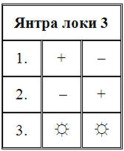
5. Возьмём пространства с равным числом полярностей. В интенсивности «умножение» тоже три полярности +, – , ☼. Это было бы равнозначно как ввести теорию групп в алгебру с операциями «сложение» и «умножение».
Так как четвёртого не дано, то такую алгебру в «умножении» составит Лока 3, то есть трёхполярное пространство. По янтре устанавливаем законы отношений : (+)*(+) = –; (–)*(–) = +; (+)*(–) = ☼.
Теперь, как и положено, в неопределённых пространствах алгебр проведём исследование. Сразу же возьмём некоторый поляризованный объект а.
Дано: в интенсивности «сложение» +а – а = 0.
В интенсивности «умножение» (+а)*(+а) = – а2; (–а)*(–а) = +а2; (+а)*(–а) = ☼а2 = а2.
Если проведём операцию в алгебре двух пространств со своими единицами, то будет (+а – а)(+а) = – а2 ^ а2. Так как + это знак полярности, то для обозначения связи здесь употреблён символ ^.
Однако по равносильности будет так же 0(+а) = ? Можно ли ставить в соответствие здесь 0? Почему возникает сомнение?
Ранее полученное – а2 ^ а2 = (+а)0. Если принять, как в современной алгебре (+а)0 = 0, то – а2 ^ а2 = 0. Появилось к исходному +а – а = 0 новое условие, откуда – а2 ^ а2 = +а – а. Если теперь (+а – а)( – а) = а2 ^ (+ а2). Откуда – а2 ^ а2 = + а2 ^ а2, то есть – а2 = + а2 . Это противоречие, когда + = –. Получилось, что в подобной алгебре (+а)0 ≠ 0, в отличие от современных алгебр.
Пространства сложения может представлять не «цепочку», а «циклическую» трёхполярность, где +а + а = – а, – а – а = +а, и +а – а = 0 . Если, если к +а – а = 0 прибавить +а, то получим (+а – а) +а = 0 + а. Откуда +2а – а = 0 + а, то есть – а – а = 0 + а, так как + а + а = – а. Отсюда, учитывая, что – а – а = + а получим + а = 0 + а. Это не противоречит пространству, так как 0 есть единица этого пространства.
Так как в трёхполярном «циклическом» пространстве при интенсивности «сложение» будет + 2а = – а, а так же – 2а = + а, окончательно +3а = – 3а = 0. Здесь Закон Сброса выражен циклом, в отличие от сброса в «цепочке», где в трёхполярности будет +а – а + ☼а = 0.
Теперь над полем изоморфных трёхполярных пространств проведём алгебру.
Возьмём для наглядности без количеств полярности ί, j, ☼ в «умножении» и ί, j, 0 в «сложении». Здесь, согласно трёхполярному пространству, ί + j = 0, 2ί = j, 2j = ί; ί*ί = j, j*j = ί, ί*j = ☼, ☼2 =☼.
Теперь (ί + j)*ί = j + ☼, затем (ί + j)* j = ί + ☼,
Следовательно, ί*0 = j + ☼, j*0 = ί + ☼. Если, как теперь принято в математике, ί*0 = 0, а так же j*0 = 0, то ί = j, что противоречит условию.
Кстати, такое противоречие не замечается в современной математике. Доказано, что имеющаяся математика противоречивая. Впрочим, это - противоречие не некоторого "действительного мира" или "алгебры действительных чисел", а двухполярного ума. По этой причине ум цивилизации Запада ведёт к деградации (см. [Человек]).
Как указывалось раньше, в подобных алгебрах для любого k условием является k*0 ≠ 0.
Из ί*0 = j + ☼, j*0 = ί + ☼ получаем 0*0*☼ = ί + j + 2☼. Если 0 + ☼ = ☼, то 0*0*☼ = ☼. В отношении единиц получилось, что единицей для этого пространства (алгебры) является 0*0. А, следовательно, 0*0 = 1,так как 1= ☼.
Можно заметить, что все алгебры, которые ассиметричные, наподобие алгебры «действительных чисел» имеют противоречие такое, что (+)*0 = 0, i*0 = 0, j*0 = 0, а*0 = 0 и т.п. Иными словами, любое «циклическое» пространство обрывает цикл на нуле. Кстати, именно в этом месте образуется противоречие, когда (+) = 0 = i = j = а = 1. О противоречивости всей современной математики уже говорилось.
Итак, имеем:
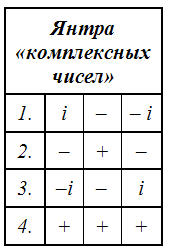
1. Алгебру действительных чисел, где двухполярное «циклическое» пространство «умножения», входит в алгебру с трёхполярной «цепочкой» в интенсивности «сложение». Аналогично построена алгебра «комплексных чисел», но так, что четырёхполярное пространство «умножения» входит в алгебру с трёхполярным пространством «сложения».
2. Аналогично возьмём трёхполярное пространство «умножения» и четырёхполярное пространство «сложения».
Здесь законы отношений будут: а) в «сложении» i + j + ☼ = 0, б) в «умножении» i*i = j, j*j = i, i*j = ☼. Отношение с единицами такое же, как и присутствует в законах пространств, то есть i + 0 = i, j + 0 = j, 0 + 0 = 0, i*0 = 0, j*0 = 0, ☼*0 = 0.
Примеры:
(iа + jа)*j = a + iа;
(iа + jа)*(iа + jа)= ja2 + a2 +a2 + ia2 = a2, то есть (iа + jа)2 = а2.
(iа + jа)3 = iа3 + jа3 (iа + jа)4 = а4.
Если число а = 1, то (i + j)*j = 1 + i; (i + j)2 = 1; (i + j)3 = i + j; (i + j)4 = 1.
В такой алгебре мы получаем своего рода циклирующее пространство «умножения» на базе пространства «сложения».
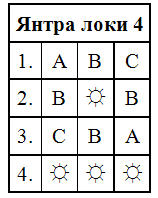
7. В этой группе алгебр будет, на очереди рассмотрения, четырёхполярное пространство «умножения», но пятиполярное пространство «сложения», где частным случаем являются «комплексные числа».
Законы отношений в пространстве «умножения» будут
(i)*(i) = – , (i)*(–) = –i , (i)*( –i) = +, (–i)*(–i) = – , (–)*(–) = + .
В пространстве «сложения» по Закону Сброса ia + ja +a – a = 0.
Алгебра «комплексных чисел» известна, хотя в своей полноте четырехполярность отличается тем, что включает известную алгебру (комплексных чисел) как частный случай.
8. Рассмотрим пятиполярное «умножение», но шестиполярное «сложение». Аналогов такой алгебры нет.
Законы отношений в «умножении» будут:
1. (А)*(В) = С, (А)*(С) = D, (А)*(D) = ☼, (А)*(А) = В, (А)3 = С, (А)4 = D, (А)*(☼) = А.
2. (В)*С) = ☼, (В)*(D) = А, (В)*(А) = С; (В)*(В) = D, (В)3 = А, (В)4 = С, (В)*(☼) = В.
3. (С)*(D) = В, (С)*(С) = А, (С)3 = D, (С)4 = В, (С)*(☼) = С.
4. (D)*(D) = C, (D)3 = B, (D)4 = A, (D)*(☼) = D.
5. (A)*(D) = (B)*(C) = ☼.
6. (A)5 = (B)5 = (C)5 = (D)5 = ☼.
Законы отношений в «цепочке» пространства «сложения» будут:
А + B + C + D + ☼ = 0.
В «цепочках» есть отношения соответствия, когда, например, A + B + ☼ = C + D.
В этом пространстве (алгебре) тоже нельзя поставить без противоречия двум элементам третий.
Пример пятиполярной алгебры над полем шестиполярного сложения.
(А + В)2 = В + 2С + D = A + C +☼ ;
(А + В)3 = С + 2D + ☼ + D + 2☼ + A = C + 3D + + 3☼ + A = B + 2D + 2☼.
(А + В)4 = D + 3☼ + 3A + B + ☼ + 3A + 3B + C = = 6A + 4B + C + D + 4☼.
С учётом Закона Сброса А + B + C + D + ☼ = 0 окончательно (А + В)4 = 5A + 3B + 3☼. Тогда (А + В)4 = 2A + 3C + 3D.
К этому примеру, (А + В)4 + 2В +2☼ + 5C + 5D = 0.
9. В шестиполярном пространстве «умножения» и семиполярном пространстве «сложения» появляются фрагменты алгебры «действительных чисел».
Здесь С*С = ☼, аналогично как (–)*(–) = +.
Поэтому в пространстве «сложения» для А + B + C + D + E + ☼ = 0 будет выполняться C + ☼ = 0, А + B + D + E = 0.
Например, (А + В)2 = В + 2С + D,
(А + В)3 = C + 3D + 3E + ☼ = 3(D + E).
Однако D + E = A + B.
Получим (А + В)3 = А + В + D + E + D + E = 0 + D + E = D + E = A + B.
(А + В)4 = (А + В)2
(А + В)5 = (А + В)3 = A + B.
Здесь в алгебре вновь появляется цикличность фрагментов «сложения». Для этого нужно, чтобы пространство «сложения» было «цепочкой».
10. Общий случай.
Условия таких алгебр следующие:
а) Пространства с интенсивностью связей «сложение» на одну полярность больше, чем пространство «умножения».
б) Пространства «сложения» суть «цепочки». Например, в алгебре «действительных чисел» +а – а = 0, но 2а – а = +а, то есть в «цепочке» есть Закон Сброса.
в) Возможны случаи, когда проявлены только некоторые законы отношений (это касается всей современной математики, где используются двухполярные свойства ума как само собой разумеющееся). Тогда необходимо, используя свойства алгебр, провести исследование для установления локальности и полного объёма отношений.