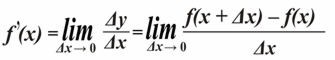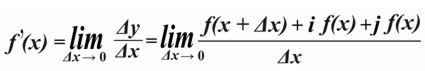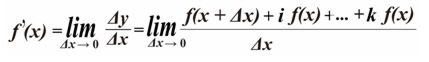Производные от поляризованных функций

Само определение производной содержит в себе поляризацию.

Если есть функция f(х), то разность f(х + Δх) – f(х) есть взаимоотношение двухполярных объектов. Кроме того, в производных есть ещё одно отношение Δу/Δх.

В современной математике чтобы получить приращение функции нужно произвести вычитание f(х + Δх) – f(х). Почему? В двухполярности только два взаимно обратных элемента.

Если обратных не два – например, в трёхполярном пространстве три взаимно обратных элемента, – то вид производной меняется.

Геометрический смысл тоже меняется.

В многополярном представлении производные могут неисчислимо «расшириться» в вариациях «сложения» и «деления». Например, трёхполярная производная в пространстве «сложения» представится как здесь полярности – ☼, ί, ј.

В общем случае производная в пространстве «сложения» будет иметь вид

здесь ☼, ί,…, k – полярности. Общим случаем является алгебра суперпозиции пространств, где функция f(w) имеет некоторое число полярных состояний – x, iy,…,kφ.