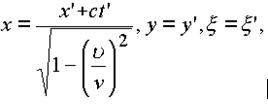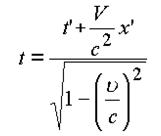Непротиворечивые алгебры
Примеры непротиворечивых алгебр
Учёные мирятся с противоречивыми алгебрами в современной математики, делая вид, что противоречия нет. Однако из 0*1 = 0, а*0 = 0, в*0 = 0, (а + в)*0 = 0 следует, что а = в = (а + в) = 0. Такое неразличение ведёт к хаосу, то есть, противоречию - сочиняй что хочешь!
Противоречия появляются в алгебрах, когда во взаимодействие вводится, как минимум, два пространства. В современных алгебрах противоречие появилось при над полем "действительных","комплексных" и прочих чисел, то есть в алгебрах с единицей.
Выход из противоречия найден В. Ленским. Алгебры могут быть (и обязаны быть) не противоречивыми.
Алгебра с одной полярностью
Начнём с алгебры с операциями «сложения» и «умножения», имеющими только один элемент ☼.
Здесь ☼*☼ = ☼, а так же ☼ + ☼ = ☼. Второго в такой алгебре не дано.
Алгебра с двумя полярностями
Янтра такого пространства будет
Чтобы не было противоречия в «сложении» должны быть тоже только две полярности. Тогда (–1) + (–1) = +1,
(+1) + (+1) = –1,
Единицей (нулём) в «сложении» будет
(+1) + (–1).
Проверим в «умножении». [(+1) + (–1)](+1) = (+1) + (–1). Сопоставим с известным нулём (единицей) в современной математике 0(+1)= 0, а так же в «сложении» [(+1) + (–1)] + [(+1) + (–1)] = [(+1) + (–1)], то есть 0 + 0 = 0. Свойства нуля «сложного» и простого совпадают.
Алгебра с тремя полярностями
Янтра такого пространства будет
В сложении имеем А + В = ☼, так как четвёртого не дано. Отсюда, А + ☼ = В, ☼ + В = А.
Из этих отношений 2А, 2В, 2☼ есть нули (единицы).
Проверим. Умножим (А + А)А = В + В, то есть тоже ноль подобно как 0*А = 0.
Для удобства нули можно различить А + А ≡ 0А , В + В ≡ 0В , ☼ + ☼ ≡ 0☼ . Однако, это условное различение, скорее, для напоминания, в действительности все нули тождественные по свойствам нуля.
Алгебра с четырьмя полярностями
Один из вариантов рассмотрен в предыдущей части, где для четырёхполярного пространства было найдено в качестве нуля 2А + 2В, 2А + 2С, 2А + 2☼,
2В + 2С, 2В + 2☼, 2С + 2☼.
Для проверки к выбранному нулю, для примера 2А + 2С прибавим В. Имеем А + А + С + С + В, где А + В + С = ☼ по условию.
Поэтому А + А + С + С + В = А + С + ☼ = В. Это равнозначно как 0 + В = В.
Возникает вопрос о сложении полярностей А + В + С + ☼. Если пятого не дано, то без противоречий можно поставить «сложный» нуль. Теперь, к примеру, А + В + С + ☼ = 2А + 2В. Отсюда С + ☼ = А + В. Добавляем А и получим А + С + ☼ = В = 2А + В. Поэтому «сложный» нуль упрощается. Теперь 2А ≡ 2В ≡ 2С ≡ 2☼ и представляют ноль.
Проверим ноль на умножение. Умножим, например, ноль (В + В) на С. Получим СВ + СВ, а по законам четырёхполярного пространства СВ + СВ = 2А, то есть ноль. Аналогично 0*С = 0.
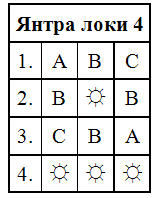
Есть ещё вариант суперпозиционной локи 4.
В этом пространстве: А + В + С = ☼, А + В + ☼ = С, А + ☼ + С = В. После преобразований получим 2А + 2В, 2А + 2С, 2С + 2В, 2А + 2☼, 2В + 2☼, 2С + 2☼ являют собой ноль. А так как для А + В + С + ☼ и пятого не дано, то нулём будут 2А ≡ 2В ≡ 2С ≡ 2☼.
Алгебра с пятью полярностями
В «сложении» пятиполярного пространства будет, например, А + В + С + D = ☼, так как шестого не дано. Из этого по правилам Янтры при умножении на А получим: В + С + D + ☼ = A, C + D + ☼ + A = B, D + ☼ + A + B = C, ☼ + F + D + C = D. Отсюда, каждая «тройка» наподобие 2А + 2В + 2С и есть нуль.
С другой стороны, для А + В + С + D + ☼ в соответствие можно поставить только 0. Значит, например, А + В + С + D + ☼ = 2А + 2В + 2С. Тогда А + В + С = D + ☼. Добавляя D + ☼, получим, что 2 D + 2☼ тоже равнозначно 0. А так как имеем, например, ноль в виде 2 D + 2☼ + 2А, то 2А тоже тождественно нулю.
Окончательно 2А ≡ 2В ≡ 2С ≡ 2D ≡ 2☼ есть нули.
Проверим по правилам Янтры на умножение. Например, (2В)С = (В + В)С = ☼ + ☼ = 2☼, то есть это подобно как 0*С = 0.
Не сложно заметить общее правило, не доказывая теоремы. Конечно, если не использовать в доказательствах выражение А + В + С + D + ☼ как конечное, то нули будут иметь иной вид.
Нули и единицы в алгебрах
Не сложно заметить, что здесь имеет место цикличность, завершающаяся на двух полярностях. Если же взять, к примеру, суперпозиционную трёхполярность, где полярностям А, В, С будут обратные полярности а, б, с, при общей единице ☼, то А*В*С = а* б* с =☼ или 0. При этом А* а = В* б = С*с = ☼ или 0.
Итак, в соответствие А + В + С можно поставить А + а, откуда В + С = а. Поэтому нулём могут быть А + а, В + б, С + с. В итоге нулями будут 3А, 3В, 3С, 3а, 3б, 3с, а так же А + а, В + б, С + с.
Всё зависит от цикличности. Если, к примеру, в локах «умножения» число единиц столько же, сколько число полярностей, то это же самое можно сказать и о пространстве «сложения», так как для любого А будет nА = А, где n – число полярностей.
Универсальных «сложных» нулей и единиц нет. Они принадлежат каждому пространству так, что спасают алгебру этого поля от противоречия.
Поэтому, «сложные» единицы и нули лучше обозначать индексами, которые укажут на пространство, где эти нули и единицы правомочны. Например, для пятиполярного пространства 05, ☼5.
В суперпозиционных алгебрах дело сложнее. Как видим из только что приведённого примера, нулями являются 3А, 3В, 3С, 3а, 3б, 3с, а так же А + а, В + б, С + с. Можно обозначить ноль этого пространства так же с индексом, но при этом указать, что оно суперпозиционное. Например, 303.
В приведённом примере единицы суперпозиционных алгебр равны А3, В3, С3, а3, б3, с3, А * а, В * б, С* с. Их можно обозначить как 3☼3, а количественную единицу как 313.
Если обратить внимание на любое пространство «умножения» с числом полярностей n, то там каждая полярность in, jn,…, kn равнозначна единице ☼. Точно так же в пространстве сложения ni, nj, …, nk равнозначны нулю.
Алгебра двух интенсивностей связи «умножения» и «сложения» будут непротиворечивыми, если число полярностей в сложении и умножении будет равно.
Для пространства «сложения» каждая из полярностей in, jn,…, kn будет единицей, как ☼ или 1.
Для пространства «умножения» каждая из полярностей ni, nj, …, nk будет нулём (0).
Число нулей и единиц будет столько же, сколько полярностей в пространстве. Возьмём, для примера, четырёхполярное пространство. Здесь для полярностей А, В, С и единицами ☼ и 0 будет 4А = 4В = 4С, а так же А4 = В4 = С4.
Следовательно, если (А + А + А + А)В, то получим в итоге ноль в виде 04.
Особое место занимают суперпозиционные пространства и харлоки, а, следовательно, алгебры суперпозиционных и харлок. Здесь нули и единицы будут иметь несколько значений; добавятся ещё перечисленным нули и единицы из взаимодействующих пространств. Примером тому является суперпозиция трёх трёхполярных пространств, где добавились нули А + а, В + б, С + с и единицы А * а, В * б, С* с.