Шестиполярное Пространство
Пространство шести полярностей
Свойства
Шестиполярное пространство будет таким же особенным; оно несёт в себе элементы двухполярных и трёхполярных законов.
Если в целом
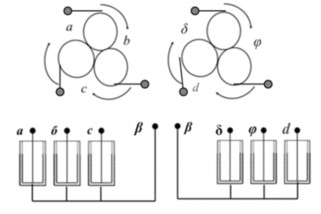
℮a + ℮b + ℮c + ℮d + ℮δ + ℮φ = β, то при этом ℮a + ℮b + ℮c = ℮d + ℮δ + ℮φ = β.
Кроме этого, в подобном пространстве выполняются законы двухполярных отношений, когда появляются три «пары» создающие образ «мира» и «антимира»:
℮a + ℮δ = β. ℮c + ℮d = β, ℮b + ℮φ = β.
Эти отношения дают возможность получения шестиполярности суперпозицией трёх «двоек» или двух «троек».
На втором каскаде осуществляется сепарация, то есть снятие «чистой» шестиполярности и выведение ёё на самостоятельное существование.
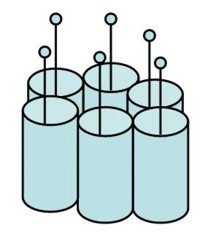
Конденсаторы
Конденсатор "лепестковый" применялся для передачи и приёма шестиполярного возмущения (волны).
Формальный аппарат
Шестиполярность косвенной генерации, то есть посредством суперпозиции описывается алгеброй «цепочек», что и было приведено раньше. В суперпозиции могут быть как однополярные, так и трёхполярные генераторы, действующие на электрофорном принципе. Поэтому, в зависимости от выбранного вида генераций, выбирается и алгебра соответствующих пространств и их суперпозиции.
Шестиполярность «прямой» генерации хорошо описывается алгеброй локи 7, которая представлена Янтрой.
Эта Янтра представляет особенное семиполярное пространство тем, что здесь три пары полярностей, которые «аннигилируют» и, вместе с тем, две «тройки», которые тоже «аннигилируют» так, что:
(А)*(F) = β, (B)*(E) = β, (C)*(D) = β; (A)*(B)*( D) = β, (C)*(E)*(F) = β.
Лока 7 всецело соответствует законам отношения цветов в свете. Если А ≡ «голубому», В ≡ «желтому», D ≡ «пурпурному», то «голубой» * «желтый» * «пурпурный» = «белый».
Если F ≡ «красному», Е ≡ «синему», С ≡ «зелёному», то
«красный» * «синий» * «зелёный» = «белый».
При этом:
«голубой» * «красный» = «белый»,
«желтый» * «синий» = «белый»,
«пурпурный» * «зелёный» = «белый».
Более того, согласно Янтры 7:
(А)*(В) = С, то есть «голубой» * «желтый» = «зелёный»,
(В)*(D) = F, то есть «желтый» * «пурпурный» = «красный»,
(A)*(D) = Е, то есть «голубой» * «пурпурный» = «синий»,
(С)*(F) = B, то есть«зелёный» * «красный» = «желтый»,
(С)*(Е) = А, то есть «зелёный» * «синий» = «голубой»,
(Е)*(F) = D, то есть «синий» * «красный» = «пурпурный».
Это и есть свойства цветов солнечного света, а, следовательно, анализатора зрения.
Как видим из работы «Зарождение Новых Миров» (см. так же Алгебра), эти алгебры хорошо описывают процессы квантовой механики.