Многополярное уравнение Шрёдингера

Уравнение Шрёдингера в четырёхполярном пространстве

Начнём с уравнения Шрёдингера для волновой функции так как оно теперь написано для четырёхполярного пространства.

Шрёдингера уравнение – основное динамическое уравнение нерелятивистской квантовой механики. Названо в честь австрийского физика Э. Шрёдингера, который предложил его в 1926. В квантовой механике Уравнение Шрёдингера играет такую же фундаментальную роль, как уравнение движения Ньютона в классической механике и Максвелла уравнения в классической теории электромагнетизма. Уравнение Шрёдингера описывает измерение во времени состояния квантовых объектов, характеризуемого волновой функцией. Если известна волновая функция ψ в начальный момент времени, то, решая уравнение Шрёдингера можно найти ψ в любой последующий момент времени t.

Тут уместно напомнить, что волновая функция взята из четырёхполярного пространства так, что при решении уравнения берётся «действительная» часть, то есть не поляризованная, из четырёх состояний пространства. В многополярной алгебре таких пространств множество и все они имеют отличающиеся решения с «действительной», то есть не поляризованной частью.

Для частицы массы m, движущейся под действием силы, порождаемой потенциалом V (х, у, z, t), уравнение Шрёдингера имеет вид:

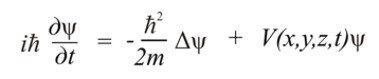,где i - мнимое число, ħ = 1,05.10^–27 эрг.сек — постоянная Планка , Δ — Лапласа оператор (х, у, z — координаты). Это уравнение называется временным уравнением Шрёдингера

Для квантовых систем, движение которых происходит в ограниченной области пространства, решения уравнения существуют только для некоторых дискретных значений энергии: E₁, E₂,..., E_n,...; члены этого ряда нумеруются набором целых квантовых чисел n. Каждому значению Еп соответствует волновая функция ψ _n (x, у, z), и знание полного набора этих функций позволяет вычислить все измеримые характеристики квантовой системы.

Уравнение Шрёдингера является математическим выражением фундаментального свойства микрочастиц — корпускулярно-волнового дуализма, согласно которому все существующие в природе частицы материи наделены также волновыми свойствами (эта гипотеза впервые была высказана Л. де Бройлем в 1924). Уравнение Шрёдингера удовлетворяет соответствия принципу и в предельном случае, когда длины волн де Бройля значительно меньше размеров, характерных для рассматриваемого движения, содержит описание движения частиц по законам классической механики. Переход от уравнения Шрёдингера к классическим траекториям подобен переходу от волновой оптики к геометрической. Аналогия между классической механикой и геометрической оптикой, которая является предельным случаем волновой, сыграла важную роль в установлении этого уравнения.

С математической точки зрения уравнение Шрёдингера есть волновое уравнение и по своей структуре подобно уравнению, описывающему колебания нагруженной струны. Однако, в отличие от решений уравнения колебаний струны, которые дают геометрическую форму струны в данный момент времени, решения ψ (х, у, z, t) уравнения Шрёдингера прямого физического смысла не имеют. Смысл имеет квадрат волновой функции, а именно величина ρ_n (x, у, z, t) = |ψ_n (x, у, z, t)|², равная вероятности нахождения частицы или системы в момент t в квантовом состоянии n в точке пространства с координатами х, у, z. Эта вероятностная интерпретация волновой функции — один из основных постулатов квантовой механики.

Трёхполярное уравнение Шрёдингера

Теперь, для примера, представим нечётное трёхполярное выражение волновой функции так как там нет четырёхполярных состояний i, –i, +, – .

Для трёх сопряженных функций будет:

f(x) = u(x) + iv(x)

f*(x) = u(x) + αv(x)

f**(x) = u(x) + φv(x)

Которые в результате дают: |f(x)|³ = f(x) f*(x) f**(x) = u(x)³ + v(x)³

Здесь «действительные» состояния равны вероятности нахождения частицы или системы в момент t в квантовом состоянии n в точке пространства с координатами х, у, z.

Математическая формулировка постулатов квантовой механики, основанная на уравнении Шрёдингера, носит название волновой механики, но, к сожалению, построена всего лишь на частном случае имеющейся на сегодня математики. Она полностью эквивалентна матричной механике В. Гейзенберга, которая была сформулирована им в 1925.

Уравнение Шрёдингера позволяет объяснить и предсказать большое число явлений атомной физики, а также вычислить основные характеристики атомных систем, наблюдаемые на опыте, например уровни энергии атомов, изменение спектров атомов под влиянием электрического и магнитного полей и т.д. С помощью этого уравнения удалось также понять и количественно описать широкий круг явлений ядерной физики, например закономерности α-распада, γ-излучение ядер, рассеяние нейтронов на ядрах и др. Детально автором это показано в труде «Построение обобщающей математической модели области применения уравнения Шрёдингера и дополнения Гоудсмита-Уленбека», Алма-Ата, 1981 г. (рукопись депонирована в КАЗНИИНТИ № Р 280).