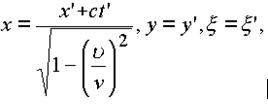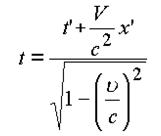Теория Относительности А.Эйнштейна
Начнем с обсуждения грубости макроскопических приборов. В 30-х годах XX-го века Альберт Эйнштейн предположил, что на самом деле происхождение квантовомеханической вероятности может быть аналогично происхождению вероятности в классической статфизике.
Напомню, что в классике вероятностное описание возникает из-за того, что мы, в силу некоторых причин, отказываемся от полной информации о системе, даваемой точными уравнениями движения, и переходим к распределениям (вероятностей) по неизвестным нам величинам.
Здесь уместно заметить, что вся «неполнота» и есть тот самый смехотворный случай, когда в дальнейшем применяют вполне определённый двухполярный математический аппарат и линейное мышление. Сами законы математического оперирования и есть та «полнота», за пределами которой нет иных полярных состояний.
Эйнштейн предположил, что все микрочастицы в дополнение к их известным характеристикам (массе, спину, зарядам, четностям) обладают набором характеристик, не доступных для измерения любым макроприбором, например, в силу грубости последнего.
Увы, но Эйнштейну не пришла в голову мысль, что измерительные приборы и мышление исследователей сами имеют вполне определённое, а не гипотетическое ограничение и область применения. Как аксиома прошло то, что имеющееся двухполярное мышление и соответствующий аппарат математики всецело соответствуют процессам Вселенной. По причине скудности ума исследователей эти характеристики назвали скрытыми параметрами квантовой теории. Таким образом, если бы физики могли изменить мышление и иметь соответствующие многополярные приборы, то можно было бы предсказать результат любого взаимодействия в микромире не вероятностным, а абсолютно детерминистичным образом. Более 30-ти лет считалось, что теорию скрытых параметров не возможно ни подтвердить, ни опровергнуть экспериментально. Действительно, как можно измерить что-то отличающееся от имеющихся у физиков средств (и ума в том числе)?
Тем не менее, 1965 году Дж. Белл предложил некоторый способ. Оказалось, что существует целый ряд экспериментальных ситуаций, в которых для определенных линейных комбинаций измеряемых на опыте величин все теории со скрытыми параметрами предсказывают результат, меньший, чем квантовая механика. При этом на возможные скрытые параметры, как микрочастицы, так и макроприбора накладывается лишь требование локальности, то есть совместимости с Теорией Относительности. Эти линейные комбинации, носящие название неравенств Белла, измерены в нескольких опытах с фотонами и протонами. Результаты опытов полностью совпали с предсказаниями квантовой механики. Исключить нелокальные скрытые параметры экспериментально не возможно. Но, с точки зрения теории, их существование противоречит Теории Относительности, правильность основных выводов которой подтверждена в сотнях экспериментов на ускорителях, в космических лучах и в атомной промышленности.
То есть, с позиции многополярности придётся переформулировать соответствующим образом Теорию Относительности.
Надо отметить, что, в понятиях многополярных пространств, преобразование Теории Относительности просто неизбежно. В многополярности возможно выбрать такие пространства, в которых, с одной стороны, не нарушается ньютоновский закон гравитации и Теория Относительности Эйнштейна, а с другой - через соответствующие измерения принципиально позволяет передавать сигналы между точками пространства быстрее скорости света. С помощью теории многополярности появилась возможность построения «причинной квантовой механики» или наоборот, поставлены эксперименты, которые позволяют окончательно опровергнуть любые теории со скрытыми параметрами.
Факт заключается в том, что предсказания многополярной квантовой механики и квантовой теории поля с экспериментальной точки зрения подтверждены гораздо точнее, чем предсказания классической механики и теории относительности.
Более того, в каком пространстве ставится эксперимент или проводятся наблюдения?
«Преобразования Лоренца» возникли на рубеже XIX-XX веков как формальный математический прием для согласования электродинамики с механикой и легли в основу Специальной Теории Относительности. Согласно этим преобразованиям длины и промежутки времени искажаются при переходе из одной системы отсчета в другую. Эти эффекты получили известность как сокращение Лоренца и замедление времени. Преобразования Лоренца явились математическим фундаментом для развития основных принципов Теории Относительности. Скорость света в Теории Относительности является предельной скоростью распространения взаимодействий, а также возможно достижимой скоростью движения материи - с = 2.988 · 1010 см/с
Из соображения «наглядности» в Теории Относительности пользуются воображаемым четырехмерным пространством, на осях которого откладываются три пространственные координаты х, у, и временная ct. Расстояние между двумя точками в таком пространстве
является интервалом между событиями 1 и 2. На базе аппарата пространственной комплексной алгебры. Координаты х, у, ξ, t в Теории Относительности преобразуются по формулам:
Принцип относительности гласит: «интервал между двумя событиями во всех инерциальных системах отсчета одинаков». Воображаемое преобразование одной системы координат к другой математически выражается как вращение четырех мерной системы. Этот физический смысл пространства установлен в геометрии Миньковского.