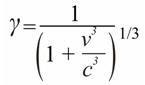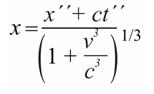Многополярная Теория Относительности

Что произошло на самом деле в преобразованиях Лоренца? Извлечение квадратного корня, как показано в «Зарождении новых миров» и в монографии «Полинарные отношения и многополярные модели» (Свердловск 1982 г.), а так же в «Преобразование Лоренца и специальной теории относительности – частные случаи многофункциональных переходов» (Алма-Ата, 1981 г. рукопись депонирована в Каз НИИНТИ № Р 258) есть «растяжение» пространства из двухполярного в четырёхполярное.

Итак, если тело, приближается к скорости света линейно, то оно согласно преобразованиям Лоренца имеет парадокс уменьшения времени (парадокс близницов).

Если теперь вместо преобразований Лоренца или Минковского применить не двух и четырёхполярные алгебры, а трёхполярную и шестиполярную алгебру. Это означает, что объект, достигая скорости света, совершает переход из трёхполярного в шестиполярное пространство. Для x = ct, x΄ = ct΄, x΄΄= ct΄΄ запишем:

Умножая правую часть таблиц, получим по законам трёхполярной алгебры c³ = γ³(с³ + v³), откуда

Координаты х, в шестиполярном переходе преобразуются по формуле:

Следовательно, при v = c искажение от перехода из трёхполярного в шестиполярное пространство будет на величину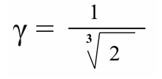

А это конкретное число и никак не предполагает увеличение массы до бесконечности или времени до нуля, как в случаях преобразований Лоренца и Минковского.

Отныне Теория Относительности должна чётко определять пространства и им соответствующие алгебры.

Такие переходы возможны в любых заданных или наблюдаемых пространствах. Однако теперь придётся чётко и осмысленно определять не только пространства, но и алгебры соответствующие им.