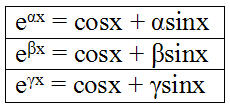Не бинарные алгебры
Поле интенсивности «сложения» может иметь любое число полярностей в пределах локи (пространства).
Например,
(ι + j + k)*(ι +j + k) = ι2 +j2 + k2 + 2(ι j + ι k + j k).
Если зададим условие ι j + ι k + j k = 0, то
(ι +j + k)2 = ι2 +j2 + k2. Такое нормирование полезно знать физикам для расширения уравнения Шрёдингера в квантовой механике.
Дальше зависит от пространства.
Если в алгебре участвовало три изоморфных двухполярных пространства, то
ι2 = j2 = k2 = ☼. Откуда (ι +j + k)2 = 3.
Если в алгебре участвовало три изоморфных трёхполярных пространства, то
(ι +j + k)2 = α + β + γ, где α2 = ι, β2 = j, γ2 = k, ιjk = 1. αβγ = 1.
Записано для наглядного сравнения с «кватернионами» (хотя «кватернионы» – система противоречивая). Такое возможно так как в таком пространстве ιj = k2, ιk = j2, jk = ι2. ι j + ι k + j k = k2 + j2 + ι2 . Отсюда для (ι +j + k)2 = ι2 +j2 + k2 + 2(ι j + ι k + j k) будет (ι +j + k)2 = 3(α + β + γ).
В приложении этому можно найти пространство, где (еαх еβх еγх)3 = е 3(α + β + γ)x .
Но так как α + β + γ = ι2 + j2 + k2 , то по теореме Пифагора для гипотенузы куба запишем α + β + γ = r2.
Теперь (еαх еβх еγх)3 = е 3(α + β + γ)x
Тема соотношения экспоненциальных и тригонометрических и функций будет рассмотрена особо.