Геометрия

Обзор

1. Геометрия имеет дело с анализатором зрения, отображенного на область того или иного вида ума. Именно поэтому важны понятия полярностей объектов. Например, в области ума есть натуральные числа, которые группируются в одной «плоскости». Однако эти числа расслаиваются, то есть выводятся в другую «плоскость», поляризацией. Это приближает ум к возможностям пространственных изображений некоторых количеств.

2. Если взять только числа 1, 2, 3, …, то они отображают пространство неполяризованных чисел. Но если взять числа «положительные» и «отрицательные», то мы имеем линейное расслоение. Так и получилось, что в историческом внедрении ума в область зрения числа стали изображать на оси. Для полного набора трёхполярных отношений должен быть ещё ноль.

…-5 -4 -3 -2 -1 0 1 2 3 4 5

3. К такому геометрическому подобию хорошо подходит двухполярная лока, где законы отношений полярностей + и − выражаются как:

а) ( + )*( + ) = ( + );

б) ( + )*( − ) = ( − );

в) ( − )*( + ) = ( + );

г) ( − )*( − ) = ( + ).

Как известно, объекты с подобными законами отношений назвали «действительными числами».

4. Впрочем, числа «положительные» и «отрицательные» уже можно отображать не на одной оси, а, например, под углом 90 градусов. Почему? Нужно всегда помнить, что в анализаторе зрения нет «положительных» и «отрицательных» объектов. Задачей является найти некоторое удобное для мышления пространственное отображение объектов ума. Это своего рода изыскательский процесс, который Р.Декарт предпочёл отображать на взаимно перпендикулярных осях.

                                              2
                                              1
                      -5  -4  -3  -2  -1  0   1  2  3  4  5         
                                             -1
                                             -2            
                        

С Декартом можно согласиться, а можно и не соглашаться при других задачах мышления.

5. Ближайшим несогласием с «декартовскими» координатами была задача отобразить «комплексные числа», то есть четырёхполярности, в законах анализатора зрения. Теперь по вертикальной оси отложили «мнимые числа».

6. Законы отношений «комплексных чисел» будут:

а) (ί)*(ί) = −;

б) (ί)*(−) = −ί;

в) (ί)*(−ί) = +;

г) (−ί)*( −ί) = −;

д) (−)*(−) = +.

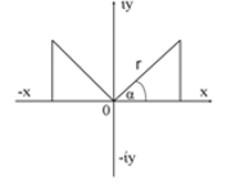
Триумфом стало то, что четырёхполярные объекты хорошо выполняют алгебру «нормирования» так, что, если взять четырёхполярную алгебру, то (х + ίу)*(х - ίу) = x²+ у² Такая алгебра «нормирования» соответствует теореме Пифагора где а² + в² = с²

Это связывает с тригонометрией так, что

сosα = х/r ; sinα = ίу/r. Поэтому (х + ίу) = r (сosα + ίsinα) называют тригонометрической формой комплексного числа.

7. Существующее геометрическое изображение «комплексных чисел» можно принять, а можно и не принять. Например, можно четырёхполярность изобразить в объёме так, что "действительные числа" будут взаимно перпендикулярны ("положительные" относительно "отрицательных"), а "мнимые числа" перпендикулярны к ним. Правомерность иных изображений обусловлена свойствами ума. Например, для трёхполярного ума подходят три взаимно перпендикулярные оси i, j, k.