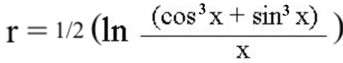Алгебры харлок (сложных пространств)
Примеры алгебр харлок
Пространства могут находиться в сложных комплексах (см. Пространства).
Для таких пространств выполнимы алгебры с двумя интенсивностями связи – «сложение» и «умножение».
Конечно, все алгебры рассмотреть не реально. Сочетаний пространств неисчислимое количество. Однако можно рассмотреть случаи те, которые покажут что вся современная математика есть частный и простенький случай МНОГОПОЛЯРНОСТИ.
Формулы Ленского
Назовём так для наглядного сопоставления с формулами Эйлера.
Из предыдущего для алгебр, где участвовало три изоморфных трёхполярных пространства, получили
(ι +j + k)2 = α + β + γ, где α2 = ι, β2 = j, γ2 = k, ιjk = 1, αβγ = 1.
В таком пространстве
ιj = k2, ιk = j2, jk = ι2. ι j + ι k + j k = k2 + j2 + ι2 .
Отсюда для (ι +j + k)2 = ι2 +j2 + k2 + 2(ι j + ι k + j k) будет (ι +j + k)2 = 3(α + β + γ).
В приложении этому можно найти пространство трёх изоморфных двухполярных алгебр, где
еαх еβх еγх = е (α + β + γ)x .
еαх = cosx + αsinx
еβх = cosx + βsinx
еγх = cosx + γsinx
С другой стороны,
еαх еβх еγх = cos3x + sin3x .
С учётом предыдущего
е (α + β + γ)x = cos3x + sin3x.
Теперь мы имеем «пучок» пространств (харлоку), алгебра которых состоит из трёх трёхполярных и трёх двухполярных пространств.
Прологарифмируем с основанием натурального логарифма. Получим (α + β + γ)x = ln (cos3x + sin3x)
Далее, так как α + β + γ = ι2 + j2 + k2 , то по теореме Пифагора для гипотенузы куба запишем
α + β + γ = r2.
Теперь r2x = ln (cos3x + sin3x).
Получили соотношение с геометрией, где радиус (гипотенуза) прямоугольника, вписанного в сферу, равен приведённой величине и зависит от угла.
Остаётся проверить совпадёт ли это пространство алгебры сложной харлоки с геометрией, построенной на свойствах анализатора зрения.
Напомню, что геометрия Лобачевского не совпадает со свойствами анализатора зрения.