Слагающие элементы: различия между версиями
Admin (обсуждение | вклад) (Новая: ==<span style="color:blue">Элементы алгебр</span>== ===<span style="color:blue">Символы</span>=== Мышление оперирует символами в вид...) |
Lenskij (обсуждение | вклад) |
||
| Строка 204: | Строка 204: | ||
б) для трёхполярного деления: | б) для трёхполярного деления: | ||
| − | [[Изображение: | + | [[Изображение: fi51.jpg]]<span style="color:blue">= а/а/а = (а)(а)<sup>ί</sup>(а)<sup>j</sup> = а<sup>(1 + ί + j)</sup> = а<sup>0</sup> = 1;</span> |
Здесь, в четырёхполярном сложении, <span style="color:blue">1 + ί + j = 0</span>; | Здесь, в четырёхполярном сложении, <span style="color:blue">1 + ί + j = 0</span>; | ||
Текущая версия на 10:05, 22 мая 2009
Элементы алгебр
Символы
Мышление оперирует символами в виде слов или некоторых обозначений. Так как слова не есть объекты действительного мира, то это тоже некоторые зрительные или звуковые символы. Например, слово «облако» это некоторый символ и не является действительным; он действителен только в мире ума. Такими символами набирается материал для мышления.
Нет символов – нет материала для мышления.
Поляризация
Символы, как объекты мышления, поляризуются по отношению друг к другу. Поляризация объектов мышления по отношению друг к другу есть неизбежное условие предстоящего процесса мышления. Назовём полярное состояние «таттвой».
Нет поляризации объектов – нет законов отношений.
Законы отношений
Законы отношений между полярностями (таттвами) или поляризованными объектами составляют природу самого мышления.
Нет отношений между объектами – нет мышления.
Пространство мышления
Законы отношений для конкретного вида ума конкретные. Они определяются числом полярных состояний в пространстве мышления. Это замкнутое числом полярностей пространство мышления назовём «лока».
Дхармы
Набор законов отношений всегда конкретен для данного пространства (локи). Пакет этих законов назовём «дхармами». Например, каким бы витиеватым и сложным не было мышление двухполярного линейного ума цивилизации Запада, оно соткано всего четырьмя дхармами.
а) (–)(–) = +;
б) (–)(+) = – ;
в) (+)(–) = –;
г) (+)(+) = +.
Любые длинные и сложные высказывания проходят этапы увязывания этими четырьмя дхармами в предложения и понятия. Например, «уничтожение созидательных условий ради злодеев, устраивающих истязания законопослушных граждан это преступление!». В символах будет: (–) (+)(–)(–)(+) = (–)!
Теперь, как бы не варьировались отношения, они будут выполняться попарно и согласно дхармам таблицы. Дискретное, парное выполнение отношений (дхарм) и создаёт линейность. Поэтому ум цивилизации Запада не только двухполярный, но и ступенчато линейный. На этой ступенчатости построена последовательность мышления, рассуждений, логики, высказываний.
Дхармы нельзя ни увеличить, ни уменьшить. У них нет ни начала, ни конца. Они не возникают и не исчезают. Как свет, проявляя другое, проявляет себя, так и дхармы проявляют себя лишь в объектах мышления, но так, что самих дхарм в том нет. «Высветить» дхармы можно лишь наблюдая за законами отношений. В приведённом примере двухполярного мышления дхармы выявлены только через двухполярное пространство мира ума.
Ядро
Так как любой объём высказываний, любые понятия и любые знания определяются и сотканы конечным числом дхарм в пространстве мышления, то это и есть ядро данного вида ума. Например, ядром двухполярного линейного ума цивилизации Запада являются приведённые в таблице четыре закона отношений, выраженные в символическом виде.
Мера
Пакет дхарм точно согласован с пространством мышления и определяет меру этого вида мышления. Например, объём знаний цивилизации Запада мнится неизмеримо огромным; он начинается с обыденных представлений и кончается научными знаниями. И, тем не менее, всё его содержание определено и гранично замкнуто всего лишь четырьмя дхармами. Ум никогда не выйдет за эту границу. Он обречён непрестанно плести паутину мысли и слагать понятия только в рамках этих четырёх дхарм. Мерой каждого вида ума является набор дхарм. Набор дхарм чётко зависит от числа полярностей в пространстве.
Граничные условия
Число дхарм в выбранном пространстве мышления нельзя ни увеличить, ни уменьшить. Если увеличить хотя бы на одну дхарму, то пространство мышления придёт в противоречие. Например, все существующие противоречия и парадоксы получились путём внедрения закона отношений из иного пространства мышления (вида ума). Если же добавить дхарму в пакет выбранного вида ума, например, двухполярного, то мышление полностью переводится в трёхполярный вид, а существующие знания аннулируются. Мера при этом снимается и устанавливается новая, соответствующая трёхполярному мышлению.
Реальность
В мире ума образованные мышлением конструкции такие же реальные, как материальные объекты в действительном мире.
Процесс мышления есть поток операций, в которых поляризованные объекты выражают отношения друг с другом. Как паучок ткёт паутину, точно так же дхармы ткут понятия.
Логика
Чёткая последовательность и чередование пакета дхарм выбранного вида пространства мышления, создаёт гарантию не противоречия. Следование по нити чередования законов отношения ума и есть логика. Каково пространство мышление, такова и логичность высказываний.
Понятия
Увязанные дхармами вариации отношений между поляризованными объектами мышления так, что удовлетворяет единству «класс». Каждый объект соотносится с этим классом и организует «сгусток», который называют «понятием».
Локализация
Число полярностей в любом пространстве счётное. Нет безграничных пространств. Если не определено пространство, то всё есть хаос. Если полагается безграничное пространство, то отношений между объектами нет. Если, по наивности или недомыслию полагается пространство неопределённым или неограниченным, но есть некоторые отношения между объектами, то это означает, что есть конкретное пространство. Устанавливается оно по законам отношений. Например, в современной математике не определяется принадлежность теорий или сконструированных моделей к двухполярному уму. Это даёт основание фантазёрству о «не конечномерных» построениях, «многомерных» алгебр и пр. Итак, если пространство изначально не определено, то законы отношений (операции) выражают его присутствие. Задачей становится определить пространство.
Поглощение
Начиная от простых отношений полярностей, пространства усложняются. Разновидности некоторых «простых» пространств уже содержат присутствие в себе законов отношений других пространств. Поэтому, как только определится класс охватываемых объектов в единство, то есть их различие в тождестве, так пространства сливаются с единой новой единицей. Например, если класс «лошади» был самостоятельным, то после перевода внимания ума на класс «животные» единица этого класса упраздняется. Такая алгебра описана в книге «Пространства».
Отношение пространств посредством отношений между полярностями этих пространств или поляризованных объектов в них и есть алгебра.
Наличие различающихся пространств, но одинаковых видов связей (интенсивности связей), полагает «простую» алгебру.
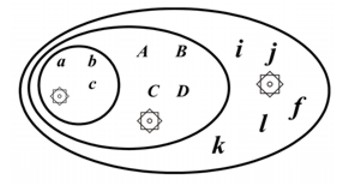
Единица
В «простой» алгебре тут же устанавливается всеобщая единица (۞). Единица есть непременный атрибут любого пространства. В книге «Пространства» обязательность единицы доказывается.
Впрочем, можно было единицу и не доказывать, так как она – свойство ума. Без охвата объектов в класс, по намеченному тождественному признаку, мышление существовать не может.
Единица ۞ и есть тот самый абсолют, который охватывает все пространства и наличествует в каждом объекте, теперь уже каждого пространства. Без охвата объектов в «класс», то есть обеспечения им единства и единичности, мышление не возможно.
Единством охвата устанавливается тождество различающихся полярностей и поляризованных объектов. На рисунке показаны три пространства. Интенсивность связи в них одна и та же. Единица у них тоже одна и та же ۞. Такая харлока есть «пучок» пространств с простой алгеброй в них. Например, возьмём пространство с объектами a, b, c как класс «лошади», а пространство с объектами A, B, C, D как «животные». Тут же второе пространство снимает единицу «лошади». Если в мышление вводится класс «биологические объекты», то он снимает единицы первых двух.
Единичность представляет количественный «эталон» каждой полярности. Именно принадлежность классу и есть единичность как количество в каждом объекте класса. Например, если в классе «лошади» можно считать только лошадей, то при охвате классом «животные» единица для счёта заменяется.
Вместе с единицей в классе тут же определяется и единичность объектов этого класса. Поэтому единица имеет сразу два лица – всеобщность и единичность.
Единство в тождестве различающихся и единичность в каждом объекте есть условие взаимоотношений, а, следовательно, условие алгебр.
Счёт
Единичность в классе позволяет считать объекты так, что при этом объединять их в группы с самостоятельным названием. Например, натуральный ряд чисел позволяет выставить ряд сгруппированных единичных объектов. При этом каждая последующая группа есть предыдущая увеличенная на единицу. При счёте единица класса «числа» не снимается. Единичность тоже остаётся постоянной. В классе «числа» счёт ведётся как операция с однополярными объектами.
Так как единица класса «числа» не есть количество, то она содержит в себе все разновидности чисел. Не понимание этого привело Бертрана Рассела к парадоксу множеств. Таким же недомыслием рождён парадокс «куча». Нашлись и те исследователи, которые заявили о «бесконечности» числовой последовательности. Это равносильно тому, что в классе «лошади» заявить о бесконечности «лошадности», потому, что найдутся лошади, отличающиеся хоть на один волосок в хвосте.
Каждое число, образованное счётом, есть самостоятельный объект класса «числа».
Сложение
От счёта сложение отличается тем, что в классе «числа» объекты могут быть поляризованы. Известной является поляризация на две противоположности. Например, можно сосчитать число «друзей» и «врагов».
В многополярности количество полярных состояний может быть разным. Например, в трёхполярности будет a, b, c вместо двухполярных + и –.
Несмотря на различное представление чисел по их счёту, число полярных состояний в пространстве постоянное. Вот почему не бывает «бесконечных» пространств. Откуда же появилось заблуждение о «бесконечности»? В сознании человека и в мышлении, в частности, есть качественное состояние потенции процесса. Ожидается беспрепятственность этого процесса. Вот это ожидание, то есть качество, и определяют как «бесконечность». Однако, по недомыслию, качество ставят в ряд с конкретными объектами. Это равносильно тому как, например, любовь поставить в ряд с килограммами.
В отличие от повсеместной двухполярности, может быть, например, ί + j + k = 0, или a + b + c + d + e = 0.
Умножение
а) (–)(–) = +;
б) (–)(+) = – ;
в) (+)(–) = –;
г) (+)(+) = +.
С операцией умножения тоже нужно внимательно разобраться. Одно дело, когда умножаются однополярные объекты (числа), но умножение полярностей имеет локальную меру. Возьмём, например, двухполярную локу. В ней: «положительные» и «отрицательные» объекты появились из психологического опыта человека. Разнополярность чисел применима в сложении. Например, было 20 баранов их них 10 чужих.
«Чужие» здесь равнозначны качественному «отрицанию», так как бараны по количеству как были, так и остались.
Другое дело, разнополярное умножение. Что станет, если 5 «своих» лошадей умножить на 10 лошадей «чужих» или на долг. По закону полярных отношений будет +5 х (– 10) = – 50. Чего (– 50)? Пятьдесят «моих чужих» лошадей? Или пятьдесят «моих долговых» лошадей? Может быть, есть отрицательные километры, площади, килограммы?
Я думаю, что отныне пора неразличений закончилась. Умножать можно объекты одинаковой полярности как числа. Например, если 5 «моих» лошадей увеличилось в 10 раз, то их будет +5 х 10 = +50, а если долг увеличился в 10 раз, то его будет –10 х 10 = – 100 лошадей.
Надеюсь, что после этого замечания исчезнут два варианта путаницы (или недомыслия): а) полярное +а и число а это не одно и то же; б) умножение полярностей это взаимодействие качеств.
Отсюда и иное отношение к законам. Например, по закону дистрибутивности (а – b)(–c) = – ac + bc. Абсурдность этого теперь очевидна. Впрочем, если «врагов» умножить на «врагов» и они станут приумноженными «друзьями», то это остаётся только приветствовать. Вот как быть с «друзьями» приумноженными во «враги»? Думаю, «отрицательные» килограммы, километры, площади, объёмы, силы тоже неуместно умножать на «отрицательные» числа, как и друзей, врагов.
Тем не менее, пространства «умножения» из-за недомыслия исследователей не пострадают. В многополярности этих пространств неисчислимо. Назначение их – взаимодействие качеств.
Категории «положительное» и «отрицательное», во все относящихся к ним разновидностях (добро, зло, друзья, враги, здоровье, болезнь и пр.), субъективные. Они не относятся к количествам, а выражают отношение к объектам, то есть качества. Эти отношения, к сожалению, пока освоены человечеством в двух полярностях «положительной» и «отрицательной».
Мышление построено так, что оно оперирует только «чистыми» полярностями». По этой причине любой объект мышления предварительно относится к одной из полярностей. В этой сортировке группируются добро, друзья, успехи, здоровье, счастье, моё, наше к «положительной» полярности, несмотря на особенность каждого объекта. То же самое свершается с «отрицательными» злом, врагами, неудачами, болезнями, несчастьем. «Оголённые» особенные и отличающиеся объекты мышления вводятся на следующем этапе во взаимоотношения согласно дхармам.
Количества могут окрашиваться полярностями (5 врагов, 1000 друзей и пр.). Например, складываются 15 положительных величин силы с 7 отрицательными величинами.
Однако поляризованные количества не входят в умножение, до этого человеческое сознание ещё не развилось.
Следует справедливости ради заметить, что в природе отмечены не только двухполярные отношения. Например, во взаимодействии «синего», «красного» и «зелёного» цветов рождается «белый». Это символически можно записать как А*В*С = ☼, так как белый цвет есть единица.
Для тройственных полярных отношений можно взять пространство, где: ί*j*k = 1, соответственно этому ί2 = j 2 = k2 = 1, ί = jk , j = ίk, k = ίj (и никакой альтернативности, как в кватернионах). Однако мышление человечества ещё не развилось до подобных отношений, а находится лишь на двухполярном базисе. Кстати, и двухполярный базис освоен ещё не полностью (см. «Тренинг»).
Деление
Деление количеств освоено человеческим умом как операция обратная умножению чисел. Чисел, и не более того.
Делить полярности подобно количествам так же нелепо, как и умножать их. Например, если (–) / (–) = +, то получится, что, к примеру, восемнадцать врагов поделённые на шесть врагов результируются тремя друзьями.
В ходе деления отрицательных сил, площадей, килограмм на отрицательные, получится такая же нелепость. Например, что получится при делении отрицательной силы, на отрицательную силу? По правилам современного деления должно получиться нечто положительное.
Однако, подобное отношение полезно для многополярного развития человеческого сознания. Правда, нужно скорректировать неразличение математиков. Если в пространстве «умножения» используются две полярности, то в пространстве «деления» их не две, как считается, а три.
Возьмём, к примеру, современную теорию групп. В ней постулируется два обратных элемента a, b таких, что a*b= е, где е – единица такая, что е*е = е. Или, в частном случае, а/а = 1.
В умножении роль единицы играет +, такой что +*+ = +. Здесь же а*а-1 = а(1-1) = а0 = 1, то есть, три полярных элемента.
Итак, для понимания полярного деления возьмём трёхполярность такую, что a*b*c = e. В частном случае будет (a)*(аί)*(а j) = а(1+ί + j)= а0= 1.
Не напрягайтесь. Если у человечества с двухполярным умом не хватила развития даже на двухполярное умножение, то на полярное деление тоже не хвати.
Запишу примеры деления при одном и том же полярном основании а так:
а) для двухполярного деления а/а = (а)(а-1) = а(1-1) = а0 = 1;
здесь в трёхполярном сложении +1 – 1 = 0;
б) для трёхполярного деления:
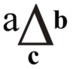 = а/а/а = (а)(а)ί(а)j = а(1 + ί + j) = а0 = 1;
= а/а/а = (а)(а)ί(а)j = а(1 + ί + j) = а0 = 1;
Здесь, в четырёхполярном сложении, 1 + ί + j = 0;