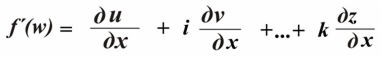Производные многих поляризованных функций: различия между версиями
Admin (обсуждение | вклад) (Новая: Многополярность имеет дело со сложными поляризованными функциями так, что после взятия производной, ...) |
Admin (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | Многополярность имеет дело со сложными поляризованными функциями так, что после взятия производной, а затем интегрирования, функции должна вернуть свой исходный вид. Начнём с не сложных примеров. Дана функция с несколькими переменными, но чётко каждая переменная находится в своей полярной плоскости: f(w) = 4х2 + 2iy + 3jg, здесь x, y, g – переменные. | + | Многополярность имеет дело со сложными поляризованными функциями так, что после взятия производной, а затем интегрирования, функции должна вернуть свой исходный вид. Начнём с не сложных примеров. Дана функция с несколькими переменными, но чётко каждая переменная находится в своей полярной плоскости: <span style="color:blue">f(w) = 4х2 + 2iy + 3jg</span>, здесь <span style="color:blue">x, y, g</span> – переменные. |
Производную находим по формуле | Производную находим по формуле | ||
| − | + | [[Изображение:Fil86.jpg]] | |
| − | |||
<span style="color:blue">f´(w) = 8x + 2i + 3j</span> | <span style="color:blue">f´(w) = 8x + 2i + 3j</span> | ||
| Строка 17: | Строка 16: | ||
Производная <span style="color:blue">f´(w) = 6ix + 15iy + i</span>. | Производная <span style="color:blue">f´(w) = 6ix + 15iy + i</span>. | ||
| − | Взяв интеграл от каждой переменной, мы получим исходную функцию. Может показаться, что под вопросом остаётся «безликое» i. Здесь проблем нет: всё, что касалось <span style="color:blue">x</span> и <span style="color:blue">y</span> то они уже определились. Остаётся любая иная переменная, как бы мы её не обозначили. | + | Взяв интеграл от каждой переменной, мы получим исходную функцию. Может показаться, что под вопросом остаётся «безликое» <span style="color:blue">i</span>. Здесь проблем нет: всё, что касалось <span style="color:blue">x</span> и <span style="color:blue">y</span> то они уже определились. Остаётся любая иная переменная, как бы мы её не обозначили. |
Обычно, при взятии интеграла, пишут ещё некоторое число, которое могло быть при взятии производной. Если и была какая-то функция или число, то они относятся только к своей полярной области и всегда будут проявлены. | Обычно, при взятии интеграла, пишут ещё некоторое число, которое могло быть при взятии производной. Если и была какая-то функция или число, то они относятся только к своей полярной области и всегда будут проявлены. | ||
Текущая версия на 09:57, 19 мая 2009
Многополярность имеет дело со сложными поляризованными функциями так, что после взятия производной, а затем интегрирования, функции должна вернуть свой исходный вид. Начнём с не сложных примеров. Дана функция с несколькими переменными, но чётко каждая переменная находится в своей полярной плоскости: f(w) = 4х2 + 2iy + 3jg, здесь x, y, g – переменные.
Производную находим по формуле
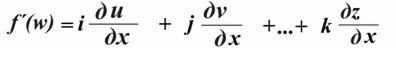
f´(w) = 8x + 2i + 3j
Забегая вперёд, можно сказать, что интеграл, то есть нахождение первообразной функции, взятый по полярностям, будет соответствовать исходной f(w).
В приведённом примере полярности определены. В дальнейшем станет понятным, что при произвольном отношении с полярностями будет полный хаос при интегрировании одних же функций, но в разных полярностях. Поэтому функции должно обозначать согласно полярностям. Например, для переменной x назначим полярность +, для y полярность i и так далее.
Может получиться так, что в одной поляризованной области окажутся две или несколько переменных величин. Например, f(w) = 3ix2 + 5iy3 + ig.
Будет вполне понятным, что речь идёт о полярной области i. Функции переменных величин обозначены по-разному, но каждая из них поляризована одинаково.
Производная f´(w) = 6ix + 15iy + i.
Взяв интеграл от каждой переменной, мы получим исходную функцию. Может показаться, что под вопросом остаётся «безликое» i. Здесь проблем нет: всё, что касалось x и y то они уже определились. Остаётся любая иная переменная, как бы мы её не обозначили.
Обычно, при взятии интеграла, пишут ещё некоторое число, которое могло быть при взятии производной. Если и была какая-то функция или число, то они относятся только к своей полярной области и всегда будут проявлены.
«Безликой» может оказаться и некоторе число. Например, если взять производную от функции по полярностям f(w) = 5x +7iy +kz , имеющей неполяризованную часть, по формуле
то получим f´(w) = 5 + 7i +k.
Ничего неопределённого и искажений такой случай не внесёт, так как интеграл будет взят по каждй части функции, то есть для каждой полярности берётся свой интеграл.
Путаница начинается, когда в одной полярной плоскости находится произведение двух переменных. Например, f(w) = 3ix2y. Производная fx´(w) = 6ixy. Если брать интеграл по dx, то исходная функция получится. Однако нам не известна переменная, поэтому, если взять интеграл по dy, то исходная функция не получается.
Именно поэтому в полярностях функций необходимо определиться чётко.
Эта проблема, то есть соответствия исходной функции и первообразной после взятия интеграла, переносится в раздел Многополярные интегралы.