Первая ступень многополярности: различия между версиями
Admin (обсуждение | вклад) (Новая: ===Линейность=== Суммирование дискретных состояний категорически отличается от линейного наращивания...) |
Admin (обсуждение | вклад) |
||
| Строка 4: | Строка 4: | ||
Последнее время началась мода на всевозможные "закручивания" тех самых линейных элементов электричества и магнетизма (рис. 1). В пример можно поставить так называемые торсионные процессы. | Последнее время началась мода на всевозможные "закручивания" тех самых линейных элементов электричества и магнетизма (рис. 1). В пример можно поставить так называемые торсионные процессы. | ||
| − | [[Изображение: | + | [[Изображение:technol_file60.jpg]] |
Рис. 1. Соленоид. | Рис. 1. Соленоид. | ||
| Строка 10: | Строка 10: | ||
"Закручивание" осуществлялось и раньше, но симметрично. Для модных "закручиваний стали использовать геометрическую несимметричность (рис.2). | "Закручивание" осуществлялось и раньше, но симметрично. Для модных "закручиваний стали использовать геометрическую несимметричность (рис.2). | ||
| − | [[Изображение: | + | [[Изображение:technol_file61.jpg]] |
Рис.2 Винт. | Рис.2 Винт. | ||
| Строка 22: | Строка 22: | ||
В пример можно привести музыку. Если частотное наращивание сделать линейным, то не будет того многообразия музыки, которое мы имеем. Дискретное разбиение линии частот на темперированный строй есть основа - основ известной музыки. | В пример можно привести музыку. Если частотное наращивание сделать линейным, то не будет того многообразия музыки, которое мы имеем. Дискретное разбиение линии частот на темперированный строй есть основа - основ известной музыки. | ||
| − | [[Изображение: | + | [[Изображение:technol_file62.jpg]] |
Рис.3 Дискретно-линейный колебательный контур Ленского. | Рис.3 Дискретно-линейный колебательный контур Ленского. | ||
| Строка 32: | Строка 32: | ||
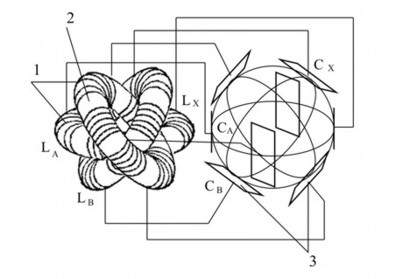
Обязательным условием того, чтобы свершались законы полярных взаимоотношений, является создание единства в локе (рис.4). | Обязательным условием того, чтобы свершались законы полярных взаимоотношений, является создание единства в локе (рис.4). | ||
| − | [[Изображение: | + | [[Изображение:technol_file63.jpg]] |
Рис.4 Единство связей. | Рис.4 Единство связей. | ||
Текущая версия на 21:58, 15 февраля 2009
Линейность
Суммирование дискретных состояний категорически отличается от линейного наращивания. Обыденные наработки в электромагнетизме направлены на оперирование величинами, но не их дискретизацией.
Последнее время началась мода на всевозможные "закручивания" тех самых линейных элементов электричества и магнетизма (рис. 1). В пример можно поставить так называемые торсионные процессы.
Рис. 1. Соленоид.
"Закручивание" осуществлялось и раньше, но симметрично. Для модных "закручиваний стали использовать геометрическую несимметричность (рис.2).
Рис.2 Винт.
Однако в этих "торсионных" схемах осталась линейность.
Дискретность
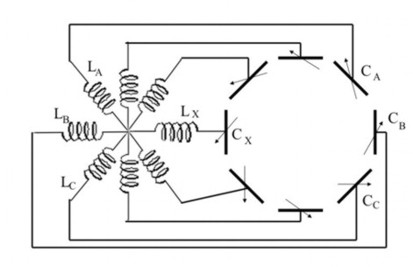
Первейшей характеристикой многополярности является дискретность. Применение дискретности к линейности создаёт преимущества поляризаций в пространстве (рис.3).
В пример можно привести музыку. Если частотное наращивание сделать линейным, то не будет того многообразия музыки, которое мы имеем. Дискретное разбиение линии частот на темперированный строй есть основа - основ известной музыки.
Рис.3 Дискретно-линейный колебательный контур Ленского.
Дискретность своим числом разрыва линейности определяет законы полярных отношений после их снятия на втором или последующих каскадах. Поэтому закон А + В + ... + Х = 0 характеризует числом Х все остальные законы взаимодействий в выбранной схеме.
Единство
Обязательным условием того, чтобы свершались законы полярных взаимоотношений, является создание единства в локе (рис.4).
Рис.4 Единство связей.
Единство выполняется общим узлом. Нужно помнить, что этот узел не следует "заземлять", так как "земля" в многополярности становится относительной. "Землёй" может быть любой объект биологического или неживой природы вида.
Пространственно-дискретные единства
Принцип новых торсионных и иных геометрических схем, основанный на дискретности, создаёт многообразие, которое, без знания задач и законов многополярности, может превратиться в хаос.
На первое место, в этой связи, выступают формальные модели (см. Математика). Знание их законов делает любой эксперимент или построение изделия осмысленными.
Линейные и иной геометрии элементы многополярных связей распространяются не только на область электромагнетизма. Наприер, при электролизе (см. Электрохимия)есть дискретность диафрагм и расщепление раствора на полярности.