Саморегулирование: различия между версиями
Kurator (обсуждение | вклад) (Новая: == Принцип саморегулирования == В ходе теоретических и экспериментальных исследований проф. В.Ленски...) |
Kurator (обсуждение | вклад) |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 2: | Строка 2: | ||
| − | В ходе теоретических и экспериментальных исследований проф. В.Ленский доказал, что все компоненты заданной локи (волнового многополярного пакета) взаимосвязаны как качественно, так и количественно. Это означает, например, что сформированная колебательным контуром Ленского волна является саморегулирующейся так, что при изменении одной или нескольких её компонентов автоматически меняют параметры остальные компоненты. Например, если в трёхполярной волне (см. рис.1 b) параметры составляющей А изменить (изменением индуктивности | + | В ходе теоретических и экспериментальных исследований проф. В.Ленский доказал, что все компоненты заданной локи (волнового многополярного пакета) взаимосвязаны как качественно, так и количественно. Это означает, например, что сформированная колебательным контуром Ленского волна является саморегулирующейся так, что при изменении одной или нескольких её компонентов автоматически меняют параметры остальные компоненты. Например, если в трёхполярной волне (см. рис.1 b) параметры составляющей <span style="color:blue">А</span> изменить (изменением индуктивности L<span style="color:blue">A</span> или ёмкости C<span style="color:blue">A</span> (см. рис.2), то автоматически изменят параметры составляющих волну <span style="color:blue">В</span> и <span style="color:blue">С</span>. |
| − | При этом постоянно будет выполнятся отношение <span style="color:blue"> | + | [[Изображение:Volni.JPG]] |
| + | |||
| + | Рис.1 Изображение волн Максвелла (а) волн (для трёхполярности)Ленского (b). | ||
| + | |||
| + | [[Изображение:Technol file777.JPG]] | ||
| + | |||
| + | Рис.2. Колебательный контур Ленского (для трёхполярных процессов). | ||
| + | |||
| + | При этом постоянно будет выполнятся отношение <span style="color:blue">Х<sub>A</sub> + Y<sub>B</sub> + Z<sub>C</sub> = 0</span> или S (где <span style="color:blue">X, Y, Z, S</span> – некоторые числа). Иными словами, сумма составляющих компонентов Х – полярной волны или многополярного сигнала всякий раз равна нулю (или некоторому постоянному числу). Принцип саморегулирования делает возможным управлять всеми компонентами Х – полярной волны посредством одной или нескольких её компонентов. Принцип саморегулирования выполняется в любом электрическом, электромагнитном, волновом виде. Это делает возможным передавать общую картину её частными составляющими без опасения интерференции волн. Например, для передаваемого звукового объёмного фантома путем снятия и передачи объёмного выражения сердечного пульса по телу человека (посредством волн Ленского), в последующем воспроизводстве звукового объёмного «тела» соответствующего сердечно-сосудистой системе этого человека, достаточно расставить систему динамиков в пространстве. В результате мы будем иметь фантом сердечно-сосудистой системы человека, но каждая составляющая передаваемой объёмной волны не есть самостоятельное отображение этого фантома. | ||
Текущая версия на 18:16, 29 мая 2009
Принцип саморегулирования
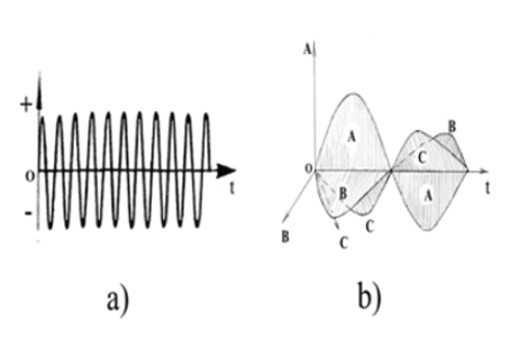
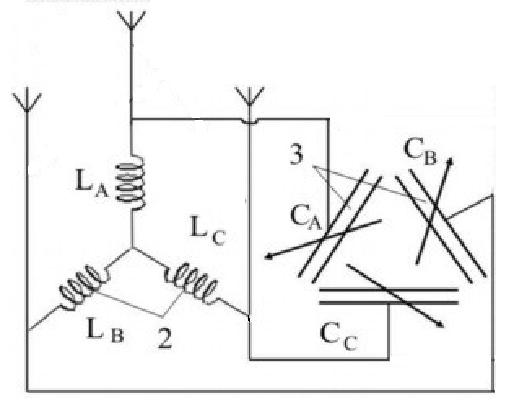
В ходе теоретических и экспериментальных исследований проф. В.Ленский доказал, что все компоненты заданной локи (волнового многополярного пакета) взаимосвязаны как качественно, так и количественно. Это означает, например, что сформированная колебательным контуром Ленского волна является саморегулирующейся так, что при изменении одной или нескольких её компонентов автоматически меняют параметры остальные компоненты. Например, если в трёхполярной волне (см. рис.1 b) параметры составляющей А изменить (изменением индуктивности LA или ёмкости CA (см. рис.2), то автоматически изменят параметры составляющих волну В и С.
Рис.1 Изображение волн Максвелла (а) волн (для трёхполярности)Ленского (b).
Рис.2. Колебательный контур Ленского (для трёхполярных процессов).
При этом постоянно будет выполнятся отношение ХA + YB + ZC = 0 или S (где X, Y, Z, S – некоторые числа). Иными словами, сумма составляющих компонентов Х – полярной волны или многополярного сигнала всякий раз равна нулю (или некоторому постоянному числу). Принцип саморегулирования делает возможным управлять всеми компонентами Х – полярной волны посредством одной или нескольких её компонентов. Принцип саморегулирования выполняется в любом электрическом, электромагнитном, волновом виде. Это делает возможным передавать общую картину её частными составляющими без опасения интерференции волн. Например, для передаваемого звукового объёмного фантома путем снятия и передачи объёмного выражения сердечного пульса по телу человека (посредством волн Ленского), в последующем воспроизводстве звукового объёмного «тела» соответствующего сердечно-сосудистой системе этого человека, достаточно расставить систему динамиков в пространстве. В результате мы будем иметь фантом сердечно-сосудистой системы человека, но каждая составляющая передаваемой объёмной волны не есть самостоятельное отображение этого фантома.
Применение
Разнообразие многополярных и псевдомногополярных форм предлагаемых В.Ленским позволяют решать вопросы объёмного цветного телевидения, создавать объёмные фантомы для слуха, получать биологические формы энергоинформационных отношений, создавать и видоизменять структуры (например, повышать октановое число горючего), исследовать аномалии Земли, производить поиски в Космосе, решать вопросы макроэнергетики и микромира (например, приведённые отношения при описании шестиполярности соответствуют законам квантовой хромодинамики и выполняются они конкретно на базе электромагнетизма).