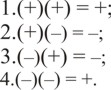Ассиметричные алгебры: различия между версиями
Admin (обсуждение | вклад) (Новая: Для понимания возьмём привычные «умножение», «деление», «сложение», «вычитание». От привычки ориент...) |
Admin (обсуждение | вклад) |
||
| Строка 9: | Строка 9: | ||
3. Тут же обращаем внимание на «умножение» в алгебре «действительных» чисел. Правила отношения полярностей всем известны: | 3. Тут же обращаем внимание на «умножение» в алгебре «действительных» чисел. Правила отношения полярностей всем известны: | ||
| − | [[Изображение: | + | [[Изображение:math_fileА1.jpg]] |
Сразу же замечаем, что здесь только две полярности. Причём (+) выполняет и роль и тождественно единице (см. [[Единица]]). | Сразу же замечаем, что здесь только две полярности. Причём (+) выполняет и роль и тождественно единице (см. [[Единица]]). | ||
| Строка 23: | Строка 23: | ||
8. Отметим <span style="color:blue">«перекос»</span>: в пространстве «сложения» участвует три полярных состояния и оно принадлежит локе 3; в пространстве «умножения» только два полярных состояния и оно принадлежит локе 2. Однако «деление» представляет локу 3. | 8. Отметим <span style="color:blue">«перекос»</span>: в пространстве «сложения» участвует три полярных состояния и оно принадлежит локе 3; в пространстве «умножения» только два полярных состояния и оно принадлежит локе 2. Однако «деление» представляет локу 3. | ||
| − | 9. Отметим также два вида «Закона сброса» (см.[[Закон сброса]]): для «сложения» и для «умножения», а именно [[Изображение: | + | 9. Отметим также два вида «Закона сброса» (см.[[Закон сброса]]): для «сложения» и для «умножения», а именно [[Изображение:math_fileА2.jpg]] для «сложения» и [[Изображение:math_fileА3.jpg]] для «умножения». Например, для комплексных чисел, то есть для локи 4 будет [[Изображение:math_fileА4.jpg]] |
| − | 10. Так как <span style="color:blue">+</span> есть полярное состояние, но представляющее единицу, то всякий раз в такой алгебре (многополярной) обязана при сбросе быть единица. Поэтому, формулу [[Изображение: | + | 10. Так как <span style="color:blue">+</span> есть полярное состояние, но представляющее единицу, то всякий раз в такой алгебре (многополярной) обязана при сбросе быть единица. Поэтому, формулу [[Изображение:math_fileА6.jpg]]можно записать как [[Изображение:math_fileА7.jpg]] так как<span style="color:blue"> <big>''na = а''</big></span>. Это правило удобно при установлении ассиметричных многополярных алгебр. |
Современная алгебра "действительных" чисел, "комплексные числа, гиперкомплексные числа и прочие есть <span style="color:blue"><big>частные случаи</big></span> многополярных ассиметричных алгебр. | Современная алгебра "действительных" чисел, "комплексные числа, гиперкомплексные числа и прочие есть <span style="color:blue"><big>частные случаи</big></span> многополярных ассиметричных алгебр. | ||
Текущая версия на 10:26, 16 февраля 2009
Для понимания возьмём привычные «умножение», «деление», «сложение», «вычитание».
От привычки ориентации на арифметику придётся отказаться, как только речь идёт не об однополярных объектах, а о нескольких полярностях и поляризованных количеств.
1. «Сложение» имеет наследие из арифметики. Пока мы группируем в «общую кучу» идут одни правила. Стоит только «вычитать», как тут же появляется полярность. Теперь действия перемещаются в плоскостную локу 2 (двухполярное пространство).
2. Так уж повелось, что в дальнейшем не стали чётко различать действия с количеством полярных состояний. Например, по Закону сброса (см.Закон сброса) даже в существующей арифметике и алгебре а – а = 0. Здесь мы имеем уже три состояния (+), (–), 0.
3. Тут же обращаем внимание на «умножение» в алгебре «действительных» чисел. Правила отношения полярностей всем известны:
Сразу же замечаем, что здесь только две полярности. Причём (+) выполняет и роль и тождественно единице (см. Единица).
4. Другое дело «деление». Обратимся к теории групп или к алгебре действительных чисел. Достаточно взять к числу а обратное число а -1, как при (а)( а -1) = 1 появилось ещё одно состояние – «единица». Например, при делении одно из чисел отрицательное, тогда получим (– 1). Итак, единица здесь есть полярное состояние.
5. Написанное выражение (а)( а -1) = 1 представляет собой Закон сброса для объёмных локальных пространств, которые называют сейчас делением.
6. В «делении» появляется третье состояние, которого нет в «умножении», а именно (+), (–), 1. Последнее не есть число 1, а представляет полярное состояние «единицу». Поэтому в теории групп его обозначили как е.
7. Теперь рассмотрим алгебру. Алгебра есть слияние «сложения» и «умножения».
8. Отметим «перекос»: в пространстве «сложения» участвует три полярных состояния и оно принадлежит локе 3; в пространстве «умножения» только два полярных состояния и оно принадлежит локе 2. Однако «деление» представляет локу 3.
9. Отметим также два вида «Закона сброса» (см.Закон сброса): для «сложения» и для «умножения», а именно ![]() для «сложения» и
для «сложения» и ![]() для «умножения». Например, для комплексных чисел, то есть для локи 4 будет
для «умножения». Например, для комплексных чисел, то есть для локи 4 будет ![]()
10. Так как + есть полярное состояние, но представляющее единицу, то всякий раз в такой алгебре (многополярной) обязана при сбросе быть единица. Поэтому, формулу ![]() можно записать как
можно записать как ![]() так как na = а. Это правило удобно при установлении ассиметричных многополярных алгебр.
так как na = а. Это правило удобно при установлении ассиметричных многополярных алгебр.
Современная алгебра "действительных" чисел, "комплексные числа, гиперкомплексные числа и прочие есть частные случаи многополярных ассиметричных алгебр.
11. Ассиметричные алгебры носят образ современных алгебр, но с большим числом полярностей. Поэтому соотношение в них двух единиц ☼ и 0 такое, что ia + 0 = ia, ☼ + 0 = ☼, а так же (ia)(☼) = ia, но между единицами (☼)(0) = 0.
12. В ассиметричной алгебре движение циклов обрывается поглощением таким, что цикл умножения прерывается нулём. Иными словами, любое (ia)(0) = 0 (см.